
分析 根据空间向量基本定理,能作为基底的向量一定是不共面的向量,由此分别分析选择.
解答 解:①若向量$\overrightarrow{a}$,$\overrightarrow{b}$与空间任意向量都不能构成基底,只能两个向量为共线向量,则$\overrightarrow{a}$∥$\overrightarrow{b}$;故①正确;
②若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$⊥$\overrightarrow{b}$,$\overrightarrow{b}$⊥$\overrightarrow{c}$,则$\overrightarrow{a}$与$\overrightarrow{c}$不确定;故②错误;
③若$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$是空间的一组基底,则A,B,C三点不共线,且$\overrightarrow{OD}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$,由空间向量基本定理得到A,B,C,D四点共面;故③正确;
④若向量$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{c}$+$\overrightarrow{a}$,是空间一组基底,则空间任何一个向量$\overrightarrow{d}$,存在唯一的实数组(x,y,z),$\overrightarrow{d}=x(\overrightarrow{a}+\overrightarrow{b})+y(\overrightarrow{b}+\overrightarrow{c})+z(\overrightarrow{c}+\overrightarrow{a})$=$(x+z)\overrightarrow{a}+(x+y)\overrightarrow{b}+(y+z)\overrightarrow{c}$,则$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$也是空间的一组基底;故④正确;
故答案为:①③④.
点评 本题考查了空间向量基本定理;理解掌握定理是解答的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
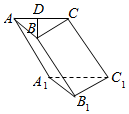 如图:在三棱柱ABC-A1B1C1中,∠A1B1C1=90°,A1B1=B1C1=AA1=2,且C在底面A1B1C1上的射影A1C1边的中点,D为AC的中点,点E在CC1上,且$\overrightarrow{{C}_{1}E}$=λ$\overrightarrow{{C}_{1}C}$(0<λ<1)
如图:在三棱柱ABC-A1B1C1中,∠A1B1C1=90°,A1B1=B1C1=AA1=2,且C在底面A1B1C1上的射影A1C1边的中点,D为AC的中点,点E在CC1上,且$\overrightarrow{{C}_{1}E}$=λ$\overrightarrow{{C}_{1}C}$(0<λ<1)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 归纳推理 | B. | 演绎推理 | C. | 类比推理 | D. | 特殊推理 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$) | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ | ||
| C. | |$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | D. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$•$\overrightarrow{b}$=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com