
设服从二项分布X~B(n,p)的随机变量X的均值与方差分别是15和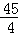 ,则n、p的值分别是( )
,则n、p的值分别是( )
A.50, | B.60, | C.50,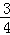 | D.60,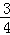 |
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)将A、B两枚骰子各抛掷一次,观察向上的点数,问:
(I)共有多少种不同的结果?
(II)两枚骰子点数之和是3的倍数的结果有多少种?
(III)两枚骰子点数之和是3的倍数的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
4位学生与2位教师并坐合影留念,针对下列各种坐法,试问:各有多少种不同的坐法?(用数字做答)
(1)教师必须坐在中间;
(2)教师不能坐在两端,但要坐在一起;
(3)教师不能坐在两端,且不能相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在二项式 的展开式中,(Ⅰ)若第5项,第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项;(Ⅱ)若前三项的二项式系数和等于79,求展开式中系数最大的项.
的展开式中,(Ⅰ)若第5项,第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项;(Ⅱ)若前三项的二项式系数和等于79,求展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
给出如下四对事件:①某人射击1次,“射中7环”与“射中8环”;
②甲、乙两人各射击1次,“甲射中7环”与“乙射中8环”;
③甲、乙两人各射击1次,“两人均射中目标”与“两人均没有射中目标”;
④甲、乙两人各射击1次,“至少有1人射中目标”与“甲射中,但乙未射中目标”,
其中属于互斥事件的有( )
| A.1对 | B.2对 | C.3对 | D.4对 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
口袋中有n(n∈N*)个白球,3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X.若P(X=2)=,则n的值为( )
| A.5 | B.6 | C.7 | D.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com