
【题目】已知点![]() ,及圆
,及圆![]() .
.
(1)求过![]() 点的圆的切线方程;
点的圆的切线方程;
(2)若过![]() 点的直线与圆相交,截得的弦长为
点的直线与圆相交,截得的弦长为![]() ,求直线的方程.
,求直线的方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)当直线斜率不存在时可知与圆相切,满足题意;当直线斜率存在时,设直线方程为![]() ,利用圆心到直线距离等于半径可构造方程求得
,利用圆心到直线距离等于半径可构造方程求得![]() ,从而得到所求切线方程;
,从而得到所求切线方程;
(2)由(1)知直线斜率必存在,设直线方程为![]() ,根据垂径定理可知圆心到直线距离
,根据垂径定理可知圆心到直线距离![]() ,从而构造出方程求得
,从而构造出方程求得![]() ,进而得到所求直线方程.
,进而得到所求直线方程.
(1)当直线斜率不存在时,方程为:![]() ,与圆相切;
,与圆相切;
当直线斜率存在时,设方程为:![]() ,即
,即![]()
![]() 圆心到直线距离
圆心到直线距离![]() ,解得:
,解得:![]()
![]() 切线方程为:
切线方程为:![]() ,即
,即![]()
综上所述:过![]() 的切线方程为:
的切线方程为:![]() 或
或![]()
(2)由(1)知,过![]() 直线与圆相交,则直线斜率必存在
直线与圆相交,则直线斜率必存在
设直线方程为:![]() ,即
,即![]()
![]() 圆心到直线距离
圆心到直线距离![]()
又相交弦长为![]() ,圆半径为
,圆半径为![]() ,则
,则![]() ,即
,即![]()
解得:![]() 或
或![]()
![]() 所求直线方程为:
所求直线方程为:![]() 或
或![]()


科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
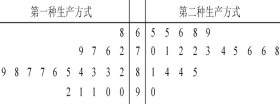
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=
的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=![]() ,E为PC的中点.
,E为PC的中点.
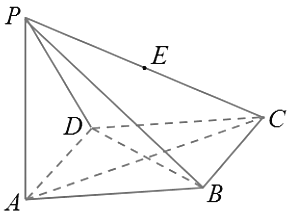
(1)求直线DE与平面PAC所成角的大小;
(2)求二面角E-AD-C平面角的正切值;
(3)在线段PC上是否存在一点M,使PC⊥平面MBD成立.如果存在,求出MC的长;如果不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,曲线C由部分椭圆C1:![]() +
+![]() =1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为![]() .
.

(1)求a,b的值;
(2)过点B的直线l与C1,C2分别交于点P,Q(P,Q,A,B中任意两点均不重合),若AP⊥AQ,求直线l
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,∠ABC=![]() ,D是棱AC的中点,且AB=BC=BB1=2.
,D是棱AC的中点,且AB=BC=BB1=2.
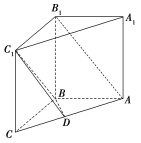
(1)求证:AB1∥平面BC1D;
(2)求异面直线AB1与BC1的夹角.
查看答案和解析>>
科目:高中数学 来源: 题型:
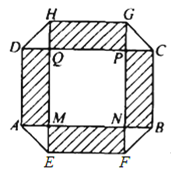
【题目】如图,居民小区要建一座八边形的休闲场所,它的主体造型平面图是由两个相同的矩形![]() 和
和![]() 构成的面积为
构成的面积为![]() 的十字形地域,计划在正方形
的十字形地域,计划在正方形![]() 上建一座花坛,造价为
上建一座花坛,造价为![]() 元/
元/![]() ;在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价为
;在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价为![]() 元/
元/![]() ;再在四个空角(图中四个三角形,如
;再在四个空角(图中四个三角形,如![]() )上铺草坪,造价为
)上铺草坪,造价为![]() 元/
元/![]()
(1)设总造价为![]() (单位:元),
(单位:元),![]() 长为
长为![]() (单位:
(单位:![]() ),试求出
),试求出![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)当![]() 长
长![]() 取何值时,总造价
取何值时,总造价![]() 最小,并求出这个最小值.
最小,并求出这个最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C:![]() 1(a>0,b>0)的左右焦点为F1,F2(|F1F2|=2c),以坐标原点O为圆心,以c为半径作圆A,圆A与双曲线C的一个交点为P,若三角形F1PF2的面积为a2,则C的离心率为_____.
1(a>0,b>0)的左右焦点为F1,F2(|F1F2|=2c),以坐标原点O为圆心,以c为半径作圆A,圆A与双曲线C的一个交点为P,若三角形F1PF2的面积为a2,则C的离心率为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com