
【题目】一批产品共10件,其中3件是不合格品,用下列两种不同方式从中随机抽取2件产品检验:
方法一:一次性随机抽取2件;
方法二:先随机抽取1件,放回后再随机抽取1件.
记方法一抽取的不合格产品数为![]() .记方法二抽取的不合格产品数为
.记方法二抽取的不合格产品数为![]() .
.
(1)求两种抽取方式下![]() ,
,![]() 的概率分布列;
的概率分布列;
(2)比较两种抽取方式抽到的不合格品平均数的大小?并说明理由.
【答案】(1)![]() ,
,![]() 的分布列见解析;(2)平均数相等,理由见解析.
的分布列见解析;(2)平均数相等,理由见解析.
【解析】
(1)![]() 可取的值为0,1,2,且
可取的值为0,1,2,且![]() 服从超几何分布,计算对应的概率,列出频率分布列;
服从超几何分布,计算对应的概率,列出频率分布列;![]() 可取的值为0,1,2,且
可取的值为0,1,2,且![]() 服从二项分布,计算对应的概率,列出频率分布列;
服从二项分布,计算对应的概率,列出频率分布列;
(2)分别计算方法一与方法二中的平均数(期望),比较结果即可.
(1)方法一中随机变量![]() 可取的值为0,1,2,且
可取的值为0,1,2,且![]() 服从超几何分布,
服从超几何分布,
于是![]() ;
;![]() ;
;
![]() ;
;
因此![]() 的频率分布可表示为下表:
的频率分布可表示为下表:
| 0 | 1 | 2 |
|
|
|
|
方法二中随机变量![]() 可取的值为0,1,2,且
可取的值为0,1,2,且![]() 服从二项分布,
服从二项分布,
于是![]() ;
;![]() ;
;
![]() ;
;
因此![]() 的频率分布可表示为下表:
的频率分布可表示为下表:
| 0 | 1 | 2 |
|
|
|
|
(2)由(1)知,方法一中![]() 的数学期望为
的数学期望为![]() ,
,
方法二中![]() 的数学期望为
的数学期望为![]() ,
,
所以两种方式抽到的不合格品平均数相等.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会于2018年11月5日至10日在上海的国家会展中心举办.国家展、企业展、经贸论坛、高新产品汇集……首届进博会高点纷呈.一个更加开放和自信的中国,正用实际行动为世界构筑共同发展平台,展现推动全球贸易与合作的中国方案.
某跨国公司带来了高端智能家居产品参展,供购商洽谈采购,并决定大量投放中国市场.已知该产品年固定研发成本30万美元,每生产一台需另投入90美元.设该公司一年内生产该产品![]() 万台且全部售完,每万台的销售收入为
万台且全部售完,每万台的销售收入为![]() 万美元,
万美元,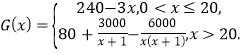
(1)写出年利润![]() (万美元)关于年产量
(万美元)关于年产量![]() (万台)的函数解析式;(利润=销售收入-成本)
(万台)的函数解析式;(利润=销售收入-成本)
(2)当年产量为多少万台时,该公司获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任利用周末时间对该班级![]() 年最后一次月考的语文作文分数进行统计,发现分数都位于
年最后一次月考的语文作文分数进行统计,发现分数都位于![]() 之间,现将所有分数情况分为
之间,现将所有分数情况分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共七组,其频率分布直方图如图所示,已知
共七组,其频率分布直方图如图所示,已知![]() .
.

(1)求频率分布直方图中![]() 、
、![]() 的值;
的值;
(2)求该班级这次月考语文作文分数的平均数和中位数.(每组数据用该组区间中点值作为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示.

(1)估计这次考试的平均分;
(2)假设分数在[90,100]的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从95,76,97,88,69,100这6个数中任取2个数,求这2个数恰好是两个学生的成绩的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解大学生对冰壶运动的兴趣,随机从某校学生中抽取了100人进行调查,经统计男生与女生的人数比为![]() ,男生中有20人表示对冰壶运动有兴趣,女生中有15人对冰壶运动没有兴趣.
,男生中有20人表示对冰壶运动有兴趣,女生中有15人对冰壶运动没有兴趣.
(1)完成![]() 列联表,并判断能否有
列联表,并判断能否有![]() 把握认为“对冰壶运动是否有兴趣与性别有关”?
把握认为“对冰壶运动是否有兴趣与性别有关”?
有兴趣 | 没有兴趣 | 合计 | |
男 | 20 | ||
女 | 15 | ||
合计 | 100 |
(2)用分层抽样的方法从样本中对冰壶运动有兴趣的学生中抽取6人,求抽取的男生和女生分别为多少人?若从这6人中选取两人作为冰壶运动的宣传员,求选取的2人中恰好有1位男生和1位女生的概率.
附:参考公式1. ,
,![]() );2.
);2. ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)设函数![]() (
(![]() ),讨论
),讨论![]() 的极值点个数;
的极值点个数;
(2)设直线![]() 为函数
为函数![]() 的图像上一点
的图像上一点![]() 处的切线,试探究:在区间
处的切线,试探究:在区间![]() 上是否存在唯一的
上是否存在唯一的![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切.
相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com