
在△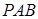 中,已知
中,已知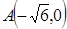 、
、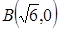 ,动点
,动点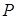 满足
满足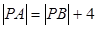 .
.
(1)求动点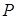 的轨迹方程;
的轨迹方程;
(2)设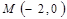 ,
,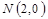 ,过点
,过点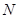 作直线垂直于
作直线垂直于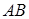 ,且与直线
,且与直线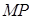 交于点
交于点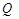 ,试在轴上确定一点
,试在轴上确定一点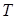 ,使得
,使得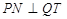 ;
;
(3)在(II)的条件下,设点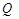 关于轴的对称点为
关于轴的对称点为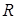 ,求
,求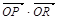 的值.
的值.
(1)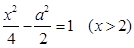 ;(2)(4,0);(3)4.
;(2)(4,0);(3)4.
【解析】本试题考查了双曲线的定义的运用,求解轨迹方程,以及直线与双曲线的位置关系的综合运用,结合数量积公式表示定值。
解:(I)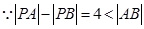 ,∴ 动点
,∴ 动点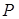 的轨迹是以
的轨迹是以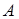 、
、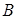 为焦点的双曲线的右支除去其与x轴的交点. …………………1分
为焦点的双曲线的右支除去其与x轴的交点. …………………1分
设双曲线方程为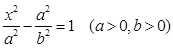 .
.
由已知,得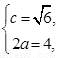 解得
解得 ∴
∴ .
∴动点
.
∴动点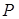 的轨迹方程为
的轨迹方程为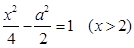 .
.
注:未去处点(2,0),扣1分
(I)
由题意,直线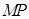 的斜率存在且不为0,设直线l的方程x =2.
的斜率存在且不为0,设直线l的方程x =2.
设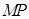 的方程为
的方程为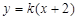 .
5分
.
5分
∵点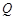 是与直线
是与直线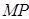 的交点,∴
的交点,∴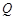
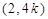 .设
.设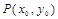
由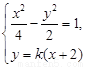 整理得
整理得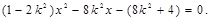
则此方程必有两个不等实根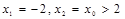
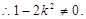 ,且
,且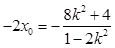 .
.
∴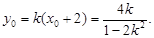 ∴
∴ .
.
设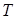
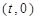 ,要使得
,要使得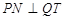 ,只需
,只需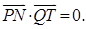
由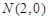 ,
, ,
,
∴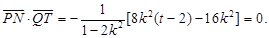
∵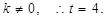 此时
此时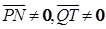 ∴所求
∴所求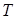 的坐标为
的坐标为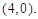
(III)由(II)知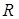
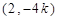 ,∴
,∴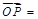
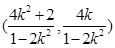 ,
,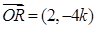 .
.
∴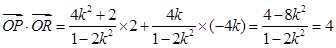 .
.
∴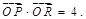


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
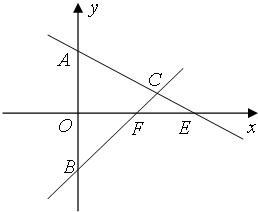 在△ABC中,已知A(0,1)、B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且
在△ABC中,已知A(0,1)、B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且| OE |
| OF |
| BC |
| CF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 6 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在△ABC中,已知A(0,1),B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且
在△ABC中,已知A(0,1),B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且| OE |
| OF |
| BC |
| CF |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
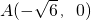 、
、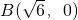 ,动点P满足|PA|=|PB|+4.
,动点P满足|PA|=|PB|+4.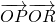 的值.
的值.查看答案和解析>>
科目:高中数学 来源:2009年北京市海淀区高考数学一模试卷(文科)(解析版) 题型:解答题
 、
、 ,动点P满足|PA|=|PB|+4.
,动点P满足|PA|=|PB|+4. 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com