
 已知一列椭圆cn:x2+
已知一列椭圆cn:x2+| y2 | ||
|
| ||
| 2 |
| ||
| n+2 |
| 1-b2 |
| 1 |
| Gn |
| 1 |
| 2 |
| 1 |
| 2 |
1-
|
| ||
| 2 |
| 1-b2 |
| 1 |
| Gn |
| 1 |
| Gn |
| 1 |
| Gn |
|
| 1 |
| 2 |
| 1 |
| 2 |
1-
|
| ||
| 2 |
| 1 |
| Gn |
| y | 2 n |
| b | 2 n |
| x | 2 n |
| G | 2 n |
| 1 |
| Gn |
| 1 | ||
|
| G | 2 n |
| G | 2 n |
| S | 2 n |
| G | 3 n |
| G | 3 n |
| 1 |
| 2 |
1±
| ||
| 6 |
| 1 |
| 2 |
1+
| ||
| 6 |
1+
| ||
| 6 |
| ||
| n+2 |
1-
|
| n+1 |
| n+2 |
| 1 |
| n+2 |
| 3 |
| 4 |
1+
| ||
| 6 |
| 4 |
| 5 |


科目:高中数学 来源: 题型:解答题
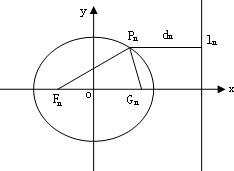 已知一列椭圆
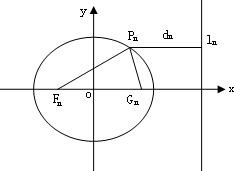
已知一列椭圆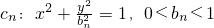 .n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点.
.n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点.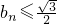 (n≥1);
(n≥1);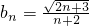 ,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).
,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).查看答案和解析>>
科目:高中数学 来源:重庆市高考真题 题型:证明题
 , 0<bn<1,n=1,2,…,若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点,
, 0<bn<1,n=1,2,…,若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是|PnFn|与|PnGn|的等差中项,其中Fn、Gn分别是Cn的左、右焦点,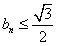 (n≥1);
(n≥1); ,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3)。
,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3)。 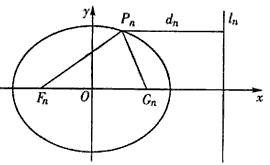
查看答案和解析>>
科目:高中数学 来源: 题型:
已知一列椭圆Cn:x2+![]() =1. 0<bn<1,n=1,2.
=1. 0<bn<1,n=1,2.![]() .若椭圆C上有一点Pn使Pn到右准线
.若椭圆C上有一点Pn使Pn到右准线![]() n的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
n的距离d.是|PnFn|与|PnCn|的等差中项,其中Fn、Cn分别是Cn的左、右焦点.
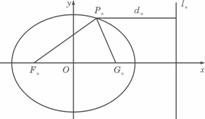 (Ⅰ)试证:bn≤
(Ⅰ)试证:bn≤![]() (n≥1);
(n≥1);
(Ⅱ)取bn=![]() ,并用SA表示
,并用SA表示![]() PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
PnFnGn的面积,试证:S1<S1且Sn<Sn+3 (n≥3).
查看答案和解析>>
科目:高中数学 来源:2006年重庆市高考数学试卷(理科)(解析版) 题型:解答题
 .n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点.
.n=1,2….若椭圆Cn上有一点Pn,使Pn到右准线ln的距离dn是{pnFn}与{PnGn}的等差中项,其中Fn、Gn分别是Cn的左、右焦点. (n≥1);
(n≥1); ,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).
,并用Sn表示△PnFnGn的面积,试证:S1<S2且Sn>Sn+1(n≥3).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com