
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,已知a=2,b=3,cosC= ![]() .
.
(1)求△ABC的面积;
(2)求sin(C﹣A)的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】若![]() 沿着三条中位线折起后能够拼接成一个三棱锥,则称这样的
沿着三条中位线折起后能够拼接成一个三棱锥,则称这样的![]() 为“和谐三角形”,设
为“和谐三角形”,设![]() 的三个内角分别为
的三个内角分别为![]() ,
, ![]() ,
, ![]() ,则下列条件不能够确定为“和谐三角形”的是
,则下列条件不能够确定为“和谐三角形”的是![]()
A. ![]() ; B.
; B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的不恒为零的函数,且对于任意实数x,y满足:f(2)=2,f(xy)=xf(y)+yf(x),an= ![]() (n∈N*),bn=
(n∈N*),bn= ![]() (n∈N*),考查下列结论:
(n∈N*),考查下列结论:
①f(1)=1;②f(x)为奇函数;③数列{an}为等差数列;④数列{bn}为等比数列.
以上命题正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如下表所示:
(天)之间的关系如下表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)请根据上表数据在所给网格纸中绘制散点图;
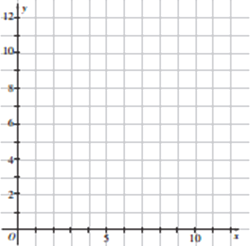
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留2位有效数字);
保留2位有效数字);
(3)根据(2)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附:  ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y= ![]() 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 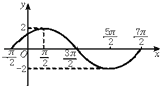
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆E: ![]() 的左焦点为F1 , 右焦点为F2 , 离心率e=
的左焦点为F1 , 右焦点为F2 , 离心率e= ![]() .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
(Ⅰ)求椭圆E的方程.
(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.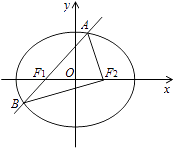
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的外接圆半径R= ![]() ,角A,B,C的对边分别是a,b,c,且
,角A,B,C的对边分别是a,b,c,且 ![]() =
= ![]()
(1)求角B和边长b;
(2)求S△ABC的最大值及取得最大值时的a,c的值,并判断此时三角形的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的首项为8,Sn是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为( )
A.S1
B.S2
C.S3
D.S4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com