【题目】已知函数
.
（1）当
时，求函数
的单调区间；
（2）若函数
的零点至少有两个，求实数
的最小值.
【答案】（1）单调递增区间为
， 
，单调递减区间为
.（2）3
【解析】（1）第（1）问，直接利用导数求函数的单调区间.(2)第（2）问， 
至少有两个根，再构造函数
，利用导数求出函数的单调区间，作出函数的图像，数形结合得到实数a的最小值.
试题解析：
（1）当
时， 
，所以有
，
令
所以当
或
时， 
， 
单调递增；
当
时， 
， 
单调递减.
故
的单调递增区间为
， 
，单调递减区间为
.
（2）令
，其在区间
内至少有两个根，则
至少有两个根，
记
，
所以
，
记
，
所以
，
令
（
舍）
所以当
时， 
， 
单调递减， 
时， 
， 
单调递增，
所以
的最小值为
，
又
，所以
时， 
，
又当
时， 
，
因此必存在唯一的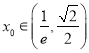
，使得
，
因此
时， 
， 
单调递增， 
， 
， 
单调递减，
时， 
， 
单调递增，画出
的大致图象，如图所示，
因此函数
的极小值为
，极大值为
，
又由于
，
因此当
时，或
时，数形结合易知函数
有2个零点，
当
时，函数
有3个零点.
综合得函数
的零点至少有两个时，实数
的最小值为3.
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知平行于
轴的动直线
交抛物线
： 
于点
，点
为
的焦点.圆心不在
轴上的圆
与直线
， 
， 
轴都相切，设
的轨迹为曲线
.
（1）求曲线
的方程；
（2）若直线
与曲线
相切于点
，过
且垂直于
的直线为
，直线
， 
分别与
轴相交于点
， 
.当线段
的长度最小时，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列是关于复数的类比推理：
①复数的加减法运算可以类比多项式的加减法运算法则；
②由实数绝对值的性质|x|2=x2类比得到复数z的性质|z|2=z2；
③已知a，b∈R，若a－b>0，则a>b类比得已知z1，z2∈C，若z1－z2>0，则z1>z2；
④由向量加法的几何意义可以类比得到复数加法的几何意义.
其中推理结论正确的是__________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列判断正确的是( )
A. 设
是实数,则“
”是“
”的充分而不必要条件
B. 
:“
,
”则有
:不存在
,
C. 命题“若
,则
”的否命题为:“若,则
”
D. “
,
”为真命题
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业从某种型号的产品中抽取了
件对该产品的某项指标
的数值进行检测，将其整理成如图所示的频率分布直方图，已知数值在100~110的产品有2l件.
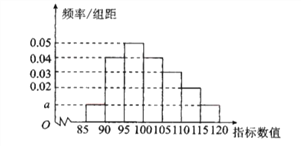
（1）求
和
的值；
（2）规定产品的级别如下表：
已知一件
级产品的利润分别为10，20，40元,以频率估计概率，现质检部门从该批产品中随机抽取两件，两件产品的利润之和为
，求
的分布列和数学期望；
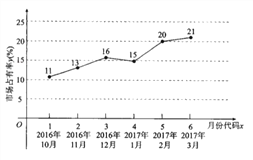
（3）为了了解该型号产品的销售状况，对该公司最近六个月内的市场占有率进行了统计，并绘制了相应的折线图，由折线图可以看出，可用线性回归模型拟合月度市场卢有率
（%）与月份代码
之间的关系.求
关于
的线性回归方程，并预测2017年4月份(即
时)的市场占有率.
(参考公式：回归直线方程为
，其中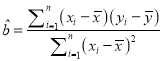
， 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，倾斜角为
的直线
经过椭圆
的右焦点且与圆
相切.
(1)求椭圆
的方程；
(2)若直线
与圆
相切于点
，且交椭圆
于
两点，射线
于椭圆
交于点
，设
的面积于
的面积分别为
.
①求
的最大值；
②当
取得最大值时，求
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
