
【题目】设p:f(x)=1+ax,在(0,2]上f(x)≥0恒成立,q函数g(x)=ax+2lnx在其定义域上存在极值.
(1)若p为真命题,求实数a的取值范围;
(2)如果“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
【答案】(1)[![]() ,+∞)(2)(﹣∞,
,+∞)(2)(﹣∞,![]() )∪[0,+∞)
)∪[0,+∞)
【解析】
(1)进行常变量分离,求出反比例函数在区间(0,2]的取值范围,最后可以求出实数a的取值范围;
(2)求出当q为真命题时, 实数a的取值范围,然后根据或命题的真假的定义,分类讨论求出实数a的取值范围.
(1)若p为真命题,则a![]() ,x∈(0,2]恒成立,所以a≥(
,x∈(0,2]恒成立,所以a≥(![]() )max,当x∈(0,2]时
)max,当x∈(0,2]时
![]() ,即a的取值范围为[
,即a的取值范围为[![]() ,+∞);
,+∞);
(2)若q为真命题:函数g(x)=ax+2lnx在其定义域上存在极值;
由于g′(x)=a![]() ,x>0
,x>0
若a≥0,g'(x)>0,g(x)在定义域单调递增,在其定义域上不存在极值,不符合题意;
若a<0,则g′(x)=a![]() 0,则x
0,则x![]() ,
,
当0<x![]() 时,g'(x)>0,g(x)单调递增;
时,g'(x)>0,g(x)单调递增;
当x![]() 时,g'(x)<0,g(x)单调递减;
时,g'(x)<0,g(x)单调递减;
∴x![]() 时,g(x)在x
时,g(x)在x![]() 时有极大值
时有极大值
所以,若q为真命题,则a<0.
因为“p或q”为真命题,“p且q”为假命题,所以命题p与q一真一假.
①p真q假时,则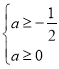 ,解得a≥0,
,解得a≥0,
②p假q真时,则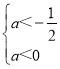 ,解得a
,解得a![]() ;
;
综上所述:a的取值范围为(﹣∞,![]() )∪[0,+∞).
)∪[0,+∞).


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知抛物线C的方程C:y2="2" p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于![]() ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
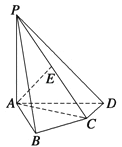
(1)求PB和平面PAD所成的角的大小;
(2)证明AE⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
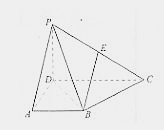
【题目】在四棱锥P—ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
(Ⅰ)求证:BE∥平面PAD;
(Ⅱ)求证:BC⊥平面PBD;
(Ⅲ)设Q为侧棱PC上一点,![]() 试确定
试确定![]() 的值,使得二面角Q—BD—P为45°.
的值,使得二面角Q—BD—P为45°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com