
焦点分别为F1,F2的椭圆![]() 过点M(2,1),抛物线
过点M(2,1),抛物线![]() 的准线过椭圆C的左焦点.
的准线过椭圆C的左焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)不过M的动直线l交椭圆C于A、B两点,若![]() •
•![]() =0,求证:直线l恒过定点,并求出该定点的坐标.
=0,求证:直线l恒过定点,并求出该定点的坐标.
考点:
直线与圆锥曲线的关系;椭圆的标准方程.
专题:
压轴题;圆锥曲线的定义、性质与方程.
分析:
(Ⅰ)由抛物线方程写出其准线方程,从而求出椭圆焦点坐标,把点M的坐标代入椭圆方程后,结合a2=b2+c2可求椭圆方程;
(Ⅱ)分直线l垂直于坐标轴和不垂直坐标轴两种情况进行讨论,直线垂直坐标轴时,把直线方程代入椭圆方程求出A,B的坐标,由![]() •
•![]() =0解出m的值,直线不垂直坐标轴时,设出直线方程的斜截式,和椭圆方程联立后由判别式大于0得到直线斜率和在y轴上的截距满足的关系式,再由
=0解出m的值,直线不垂直坐标轴时,设出直线方程的斜截式,和椭圆方程联立后由判别式大于0得到直线斜率和在y轴上的截距满足的关系式,再由![]() •
•![]() =0把直线的截距用斜率表示,代回直线方程后由线系方程可得直线恒过定点.
=0把直线的截距用斜率表示,代回直线方程后由线系方程可得直线恒过定点.
解答:
(Ⅰ)解:由2p=![]() ,∴p=
,∴p=![]() ,∴抛物线
,∴抛物线![]() 的准线方程为
的准线方程为![]() .
.
故![]() ,
,![]() ,
,
∴椭圆方程可化为![]() ,又椭圆过点M(2,1),
,又椭圆过点M(2,1),
∴![]() ,则a4﹣8a2+12=0,
,则a4﹣8a2+12=0,
∵a2>3,解得:a2=6.
∴所求椭圆的方程为![]() .
.
(Ⅱ)证明:①若直线l⊥x轴,直线l可设为x=m(m≠2),则直线l与椭圆交于
![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
即3m2﹣8m+4=0.
解得:m=2(舍)或![]() ,
,
故直线l的方程为![]() .
.
②若直线l与x轴不垂直,可设直线l的方程为y=kx+n.
直线l与椭圆![]() 交于A(x1,y1),B(x2,y2).
交于A(x1,y1),B(x2,y2).
由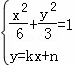 ⇒(1+2k2)x2+4knx+2n2﹣6=0.
⇒(1+2k2)x2+4knx+2n2﹣6=0.
由△>0,得:(4kn)2﹣4(1+2k2)(2n2﹣6)>0,即6k2﹣n2+3>0.
由根与系数关系得:![]() ,
,![]() .
.
由![]() 得:(x1﹣2)(x2﹣2)+(y1﹣1)(y2﹣1)=0,
得:(x1﹣2)(x2﹣2)+(y1﹣1)(y2﹣1)=0,
即x1x2﹣2(x1+x2)+y1y2﹣(y1+y2)+5=0,
又y1=kx1+n,y2=kx2+n,
故![]() ,
,
即![]() .
.
∴4k2+8kn+(3n+1)(n﹣1)=0,即(2k+3n+1)(2k+n﹣1)=0.
∴![]() 或n=﹣2k+1.
或n=﹣2k+1.
而![]() 或n=﹣2k+1满足△>0.
或n=﹣2k+1满足△>0.
∴直线l为![]() 或y=kx﹣2k+1=k(x﹣2)+1.
或y=kx﹣2k+1=k(x﹣2)+1.
由于直线l不过M,∴直线y=kx﹣2k+1=k(x﹣2)+1不合题意.
∴直线l为![]() .
.
综合①②,直线l为为![]() 或
或![]() .
.
故直线l恒过定点![]() .
.
点评:
本题考查了椭圆标准方程的求法,考查了直线和圆锥曲线的位置关系,考查了分类讨论的数学思想,证明直线l恒过定点时,综合考查了向量知识、直线系方程及学生的运算能力,此题属难题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
| F1M |
| F1A |
| F1B |
| F1O |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| PF2 |
| F1F2 |
| OH |
| PF1 |
| OH |
| OF1 |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com