
【题目】已知椭圆![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() ,已知其离心率为
,已知其离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆的标准方程.
(2)设![]() ,
,![]() 是椭圆上位于
是椭圆上位于![]() 轴上方的两点,且直线
轴上方的两点,且直线![]() 与直线
与直线![]() 平行,
平行,![]() 与
与![]() 交于点
交于点![]() ,探究
,探究![]() 是否为定值?如果为定值,请求出该定值;如果不为定值,请说明理由.
是否为定值?如果为定值,请求出该定值;如果不为定值,请说明理由.
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】已知点A,B,C,D是直角坐标系中不同的四点,若![]() ,
,![]() ,且
,且![]() ,则下列说法正确的是( ),
,则下列说法正确的是( ),
A.C可能是线段AB的中点
B.D可能是线段AB的中点
C.C、D可能同时在线段AB上
D.C、D不可能同时在线段AB的延长线上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东方商店欲购进某种食品(保质期一天),此商店每两天购进该食品一次(购进时,该食品为刚生产的).根据市场调查,该食品每份进价![]() 元,售价
元,售价![]() 元,如果一天内无法售出,则食品过期作废,现统计该产品
元,如果一天内无法售出,则食品过期作废,现统计该产品![]() 天的销售量如下表:
天的销售量如下表:

(1)根据该产品![]() 天的销售量统计表,求平均每天销售多少份?
天的销售量统计表,求平均每天销售多少份?
(2)视样本频率为概率,以一天内该产品所获得的利润的平均值为决策依据,东方商店一次性购进![]() 或
或![]() 份,哪一种得到的利润更大?
份,哪一种得到的利润更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20世纪70年代,流行一种游戏——角谷猜想,规则如下:任意写出一个自然数![]() ,按照以下的规律进行变换,如果
,按照以下的规律进行变换,如果![]() 是奇数,则下一步变成
是奇数,则下一步变成![]() ;如果
;如果![]() 是偶数,则下一步变成
是偶数,则下一步变成![]() ,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,下列程序框图就是根据这个游戏而设计的,如果输出的
,这种游戏的魅力在于无论你写出一个多么庞大的数字,最后必然会落在谷底,下列程序框图就是根据这个游戏而设计的,如果输出的![]() 的值为6,则输入的
的值为6,则输入的![]() 值可以为( )
值可以为( )
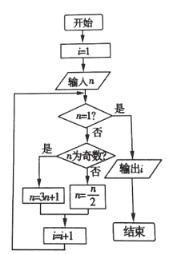
A. 5或16B. 16C. 5或32D. 4或5或32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点.
两点.
(1)求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)若线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于
轴于![]() ,求证:
,求证:![]() ;
;
(3)若直线![]() 的斜率依次为
的斜率依次为![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,线段
,…,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点依次为
轴的交点依次为![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,求
,…,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 、
、![]() ,其中,
,其中,![]() ,数列{bn}满足b1=2,bn+1=2bn.
,数列{bn}满足b1=2,bn+1=2bn.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在自然数![]() ,使得对于任意
,使得对于任意![]() ,
,![]() ,有
,有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;
的最小值;
(3)若数列![]() 满足
满足![]()
 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com