练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题满分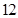分）（理科）在线段AD上任取不同于A，D的两点B，C，在B，C处折断此线段得到一条折线。求此折线能构成三角形的概率。

     

     

    【答案】

    解法1：设AD长为1，折断后三段长分别是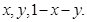则此不等式组表示的平面区域为如图1所示的的内部。这样的点对应于试验的所有可能结果。

    设“以为边能构成三角形”为事件A，则A发生当且仅当满足即图中的内部。

    这是一个几何概型问题，故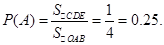

    解法2：设AD长为1,AB，AC的长度分别为x，y。上于B，C在线段AD上，因而应有0≤x，y≤1。由此可见，点对（B，C）与正方形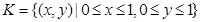内的点（x,y）是一一对应的。

    当x<y时，这时AB，BC，CD能构成三角形的充要条件是AB+BC>CD，BC+CD>AB，CD+AB>BC。因为AB＝x，BC＝y-x，CD＝1-y，代入上面三式，得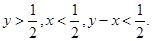符合此条件的点（x,y）必落在（图2）。同样地，当时，当且仅当点落在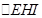中时，AC，CB，BD能构成三角形。由几何概型的公式可知，所求的概率为

    △GFE的面积+△EHI的面积

    正方形K的面积

    ＝

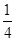
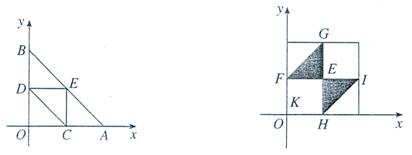
    （图1）                         （图2）

     

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本题满分16分）

       （文科学生做）已知命题p：函数在R上存在极值；

    命题q：设A={x| x 2 + 2 x 3<0}, B={x| x 2 (a +１) x + a >0}，若对，都有；

    若为真，为假，试求实数a的取值范围。

     

    （理科学生做）已知命题p：对，函数有意义；

    命题q：设A={x| x 2 + 2 x 3<0}, B={x| x 2 (a +１) x + a >0}，若对，都有；

    若为真，为假，试求实数a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分12分）【理科】已知函数

       （I）求的极值；

       （II）若的取值范围；

       （III）已知

    查看答案和解析>>

    科目：高中数学 来源：2013届江苏省扬州市高二下期中数学试卷（解析版） 题型：解答题

    （本题满分15分）本题理科做.

    设，（、）。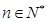

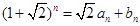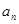    （1）求出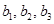的值；

    （2）求证：数列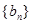的各项均为奇数.

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年四川省成都市高二3月月考数学试卷 题型：填空题

    （文科做）（本题满分14分）如图，在长方体

    ABCD—A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动.

    （1）证明：D1E⊥A1D;

    （2）当E为AB的中点时，求点E到面ACD1的距离；

    （3）AE等于何值时，二面角D1—EC－D的大小为.　　　　　　　　　　　　　　　　　　　　　　

     

     

     

    （理科做）(本题满分14分)

         如图，在直三棱柱ABC – A1B1C1中，∠ACB = 90°，CB = 1，

    CA =，AA1 =，M为侧棱CC1上一点，AM⊥BA1．

       （Ⅰ）求证：AM⊥平面A1BC；

       （Ⅱ）求二面角B – AM – C的大小；

       （Ⅲ）求点C到平面ABM的距离．

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案