
分析 (1)p=1,q=0时,$\frac{{S}_{n}}{{a}_{n}}$=n,可得Sn=nan,n≥2时,an=Sn-Sn-1,化为:an=an-1,即可证明.
(2)设等差数列{an}的公差为d,可得Sn=na1+$\frac{n(n-1)}{2}$d,an=a1+(n-1)d.
又$\frac{{S}_{n}}{{a}_{n}}$=pn+q,可得na1+$\frac{n(n-1)}{2}$d=(pn+q)[a1+(n-1)d](*).比较两边的系数可得:$\frac{d}{2}$=pd,对d 分类讨论,进而得出.
(3)由$\frac{{S}_{1}}{{a}_{1}}$=p+q=1,可得q=1-p.由Sn=(pn+1-p)an,利用递推关系可得:p(n-1)an=(pn+1-2p)an-1,即$\frac{{a}_{n}}{pn+1-2p}=\frac{{a}_{n-1}}{p(n-1)}$.必要性:当p=$\frac{1}{2}$时,$\frac{{a}_{n}}{n}=\frac{{a}_{n-1}}{n-1}$(n≥2)可得a2016=2016a1.充分性:反证法,当p$>\frac{1}{2}$时,可得$\frac{{a}_{2016}}{2016}$$<\frac{{a}_{1}}{1}$,不满足a2016=2016a1.当p$<\frac{1}{2}$时,同理可证明,不满足a2016=2016a1.
解答 (1)证明:p=1,q=0时,$\frac{{S}_{n}}{{a}_{n}}$=n,可得Sn=nan,n≥2时,an=Sn-Sn-1=nan-(n-1)an-1,
化为:an=an-1,
∴an=a1,∴{an}是等差数列.
(2)解:设等差数列{an}的公差为d,∴Sn=na1+$\frac{n(n-1)}{2}$d,an=a1+(n-1)d.
则$\frac{{S}_{n}}{{a}_{n}}$=$\frac{n{a}_{1}+\frac{n(n-1)d}{2}}{{a}_{1}+(n-1)d}$=pn+q,∴na1+$\frac{n(n-1)}{2}$d=(pn+q)[a1+(n-1)d](*).
比较两边的系数可得:$\frac{d}{2}$=pd,
当d=0时,na1=a1(pn+q),解得p=1,q=0.
此时,Sn=nan,由(1)可得:{an}是等差数列.
当d≠0时,p=$\frac{1}{2}$.由(*)比较常数项可得:0=(a1-d)q,
则d=a1,an=nd,{an}是等差数列.综上可得:p=1或$\frac{1}{2}$.
(3)证明:由$\frac{{S}_{1}}{{a}_{1}}$=p+q=1,可得q=1-p.
由Sn=(pn+1-p)an,Sn-1=(pn+1-2p)an-1(n≥2),
相减可得:p(n-1)an=(pn+1-2p)an-1,即$\frac{{a}_{n}}{pn+1-2p}=\frac{{a}_{n-1}}{p(n-1)}$.
必要性:当p=$\frac{1}{2}$时,$\frac{{a}_{n}}{n}=\frac{{a}_{n-1}}{n-1}$(n≥2).∴$\frac{{a}_{2016}}{2016}$=$\frac{{a}_{2015}}{2015}$=…=$\frac{{a}_{1}}{1}$,
∴a2016=2016a1.
充分性:反证法,当p$>\frac{1}{2}$时,由p(n-1)an=(pn+1-2p)an-1=pnan-1+(1-2p)an-1(n≥2),
又数列各项为正数,∴p(n-1)an<(1-2p)an-1(n≥2),即$\frac{{a}_{n}}{n}$$<\frac{{a}_{n-1}}{n-1}$,
∴$\frac{{a}_{2016}}{2016}$$<\frac{{a}_{1}}{1}$,不满足a2016=2016a1.当p$<\frac{1}{2}$时,
同理可证明,不满足a2016=2016a1.
点评 本题考查了充要条件的判定、方程的解法、反证法、分类讨论方法、等差数列的定义通项公式与求和公式,考查了推理能力,属于难题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪(2,+∞) | B. | (1,2) | C. | [1,2) | D. | (-∞,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.952 | B. | 0.942 | C. | 0.954 | D. | 0.960 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | ±1 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
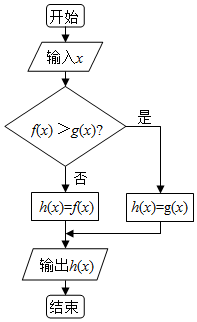
| A. | 2016 | B. | 2017 | C. | logπ2016 | D. | ln2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
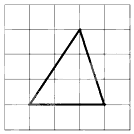
| A. | $\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $\frac{9}{2}$ | D. | $\frac{9}{2}\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com