练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情






    (1)求函数的解析式和定义域，并判断函数的奇偶性(不必说明理由)；
    (2)若方程恰有一个零点，求的值
    （1）为奇函数 （2）或
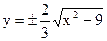
    （1）∵  ∴……………………1分
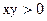
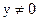
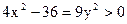
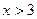
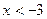
    又故  由  则或…………………2分
    ∴……………………………………4分
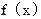
    容易知为奇函数……………………………………6分
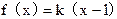
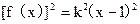
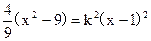
    （2）∵  ∴ 即可化为
    ……………………………………8分
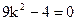
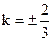
    当 即时，方程为
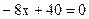
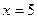
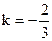
    方程只有一个零点代入检验只有 符合要求…………………10分
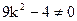
    当时，方程为一元二次方程，要使方程恰有一个零点则
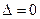
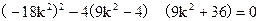
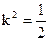
    即解得即
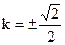
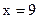
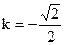
    此时代入检验只有符合要求…………………………………11分
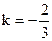
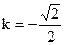
    故或…………………………………12分
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

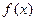
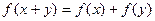
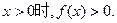
    已知定义在R上的函数，对于任意实数x，y都满足，且当试判断函数的奇偶性与单调性，证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题







    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

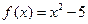
    用二分法求函数的一个正零点（误差不超过）．

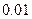
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    判断下列各函数的奇偶性：
    （1）f（x）=（x-2）；
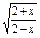
    （2）f（x）=；
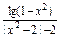
    （3）f（x）=

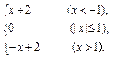
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知奇函数f(x)是定义在(－3，3)上的减函数，且满足不等式f(x－3)+f(x2－3)<0,设不等式解集为A，B=A∪{x|1≤x≤},求函数g(x)=－3x2+3x－4(x∈B)的最大值。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

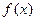
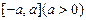
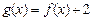
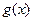
    已知函数是定义在区间上的奇函数，若，则的最大值与最小值之和为                               （   ）
    A．0B．2C．4D．不能确定

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若函数分别是上的奇函数、偶函数，且满足，则有
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知f (x)是定义在实数集R上的函数，且满足，，
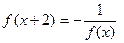
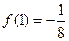
    则f (2007)=__________．

    查看答案和解析>>

    同步练习册答案