
【题目】如图,在四棱锥![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
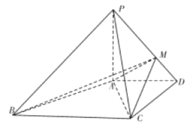
(1)取![]() 中点
中点![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
(3)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,如果存在,求
,如果存在,求![]() 与平面
与平面![]() 所成角,如果不存在,请说明理由.
所成角,如果不存在,请说明理由.
【答案】(1)见解析(2) ![]() (3)见解析
(3)见解析
【解析】
试题分析:(1)建立如图所示的坐标系,先求![]() 的方向向量,再出利用向量垂直数量积为零,列方程组求出平面
的方向向量,再出利用向量垂直数量积为零,列方程组求出平面![]() 的法向量
的法向量![]() ,由
,由![]() 可得结果;(2)分别求出直线
可得结果;(2)分别求出直线![]() 与
与![]() 的方向向量,利用空间向量夹角余弦公式可得直线
的方向向量,利用空间向量夹角余弦公式可得直线![]() 与
与![]() 所成角的余弦值(结果注意取绝对值);(3)
所成角的余弦值(结果注意取绝对值);(3)![]() ,
,![]() ,分别根据向量垂直数量积为零列方程组求出平面
,分别根据向量垂直数量积为零列方程组求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得
的一个法向量,根据空间向量夹角余弦公式,可得![]() ,从而可确定
,从而可确定![]() 的坐标,利用
的坐标,利用![]() 可得结果.
可得结果.
试题解析:如图建系:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
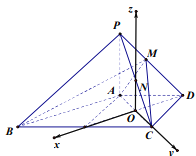
(1)![]() 中点
中点![]() ,
,
∴![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() ,
,![]() ,
,
可得:![]() ,∴
,∴![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)![]() ,
,![]() ,
,
∴![]() .
.
(3)设![]() 及
及![]() ,
,
∴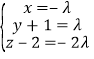
![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
,![]() 可得
可得![]() ,
,
平面![]() 的法向量为
的法向量为![]() ,
,
∴![]()
![]() ,
,
解得![]() .
.
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]()
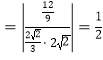 ,∴
,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】给定函数![]() 和
和![]() ,若存在常数
,若存在常数![]() ,
,![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域
对其公共定义域![]() 的任何实数
的任何实数![]() 分别满足
分别满足![]() 和
和![]() ,则称直线
,则称直线![]() :
:![]() 为函数
为函数![]() 和
和![]() 的“隔离直线”,给出下列四组函数:
的“隔离直线”,给出下列四组函数:
(1)![]() ,
,![]() ; (2)
; (2)![]() ,
,![]() ;
;
(3)![]() ,
,![]() ; (4)
; (4)![]() ,
,![]() ;
;
其中函数![]() 和
和![]() 存在“隔离直线”的序号是( )
存在“隔离直线”的序号是( )
A.(1)(3)B.(1)(3)(4)C.(1)(2)(3)D.(2)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节过后,甲、乙、丙三人谈论到有关![]() 部电影
部电影![]() ,
,![]() ,
,![]() 的情况.
的情况.
甲说:我没有看过电影![]() ,但是有
,但是有![]() 部电影我们三个都看过;
部电影我们三个都看过;
乙说:三部电影中有![]() 部电影我们三人中只有一人看过;
部电影我们三人中只有一人看过;
丙说:我和甲看的电影有![]() 部相同,有
部相同,有![]() 部不同.
部不同.
假如他们都说的是真话,则由此可判断三部电影中乙看过的部数是( )
A.![]() 部B.
部B.![]() 部C.
部C.![]() 部D.
部D.![]() 部或
部或![]() 部
部
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某大学学生的某天上网的时间,随机对![]() 名男生和
名男生和![]() 名女生进行了不记名的问卷调查.得到了如下的统计结果:
名女生进行了不记名的问卷调查.得到了如下的统计结果:
表1:男生上网时间与频数分布表
上网时间(分钟) |
|
|
|
|
|
人数 |
|
|
|
|
|
表2:女生上网时间与频数分布表
上网时间(分钟) |
|
|
|
|
|
人数 |
|
|
|
|
|
(1)用分层抽样在![]() 选取
选取![]() 人,再随机抽取
人,再随机抽取![]() 人,求抽取的
人,求抽取的![]() 人都是女生的概率;
人都是女生的概率;
(2)完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“大学生上网时间与性别有关”?
的把握认为“大学生上网时间与性别有关”?
上网时间少于 | 上网时间不少于 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: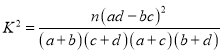
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三角形的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,则该三角形的重心(三边中线交点)的坐标为
,则该三角形的重心(三边中线交点)的坐标为![]() .类比这个结论,连接四面体的一个顶点及其对面三角形重心的线段称为四面体的中线,四面体的四条中线交于一点,该点称为四面体的重心.若四面体的四个顶点的空间坐标分别为
.类比这个结论,连接四面体的一个顶点及其对面三角形重心的线段称为四面体的中线,四面体的四条中线交于一点,该点称为四面体的重心.若四面体的四个顶点的空间坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则该四面体的重心的坐标为( )
,则该四面体的重心的坐标为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:

以这80名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率.
(1)从这80名点外卖的用户中任取一名用户.求该用户的送餐距离不超过3千米的概率;
(2)试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐贽用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份5元;超过4千米为远距离,每份9元,若送餐员一天的目标收 人不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com