
���� ��1���������������г��������n��ֵ��
��2��������֪��ȡֵΪ3��4��5��6�������Ӧ�ĸ���ֵ��д���εķֲ��к���ѧ����ֵ��
��� �⣺��1��������֪��$\frac{{C}_{n+1}^{1}{•C}_{2}^{1}}{{C}_{n+3}^{2}}$=$\frac{8}{15}$��
������2n2-5n-3=0��
���n=3��n=-$\frac{1}{2}$���������⣬��ȥ����
��n=3��
��2��������֪��ȡֵΪ3��4��5��6��
P����=3��=$\frac{{C}_{1}^{1}{•C}_{2}^{1}}{{C}_{6}^{2}}$=$\frac{2}{15}$��
P����=4��=$\frac{{C}_{2}^{2}{+C}_{1}^{1}{•C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{4}{15}$��
P����=5��=$\frac{{C}_{2}^{1}{•C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{6}{15}$=$\frac{2}{5}$��
P����=6��=$\frac{{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{3}{15}$=$\frac{1}{5}$��
��εķֲ���Ϊ��
| �� | 3 | 4 | 5 | 6 |
| P | $\frac{2}{15}$ | $\frac{4}{15}$ | $\frac{2}{5}$ | $\frac{1}{5}$ |
���� ���⿼����ɢ����������ķֲ��к���ѧ�����������⣬����ʱҪע���������֪ʶ�ĺ������ã����ۺ��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1+i | B�� | 1-i | C�� | 2i | D�� | -2i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 5 | C�� | -3 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{\sqrt{5}}{3}$ | B�� | -$\frac{\sqrt{2}}{3}$ | C�� | $\frac{\sqrt{5}}{3}$ | D�� | $\frac{\sqrt{2}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
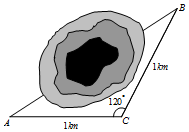 ��ͼ���ڸ��ٹ�·��������Ҫȷ�������ij��ȣ����̼�����Ա�Ѳ���������˵�����A��B����C�ľ���AC=BC=1km���ҡ�ACB=120�㣬��A��B�����ľ���Ϊ��������
��ͼ���ڸ��ٹ�·��������Ҫȷ�������ij��ȣ����̼�����Ա�Ѳ���������˵�����A��B����C�ľ���AC=BC=1km���ҡ�ACB=120�㣬��A��B�����ľ���Ϊ��������| A�� | $\sqrt{3}$km | B�� | $\sqrt{2}$km | C�� | 1.5km | D�� | 2km |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com