
已知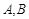 是椭圆
是椭圆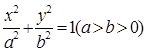 和双曲线
和双曲线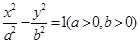 的公共顶点。
的公共顶点。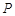 是双曲线上的动点,
是双曲线上的动点,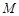 是椭圆上的动点(
是椭圆上的动点(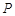 、
、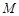 都异于
都异于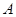 、
、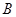 ),且满足
),且满足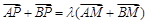 ,其中
,其中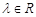 ,设直线
,设直线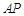 、
、 、
、 、
、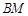 的斜率分别记为
的斜率分别记为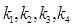 ,
, 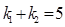 ,则
,则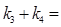
-5
解析试题分析:设出点P、M的坐标,代入双曲线和椭圆的方程,再利用已知满足 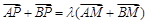
及其斜率的计算公式即可求出.解:∵A,B是椭圆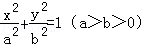 和双曲线
和双曲线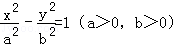 的公共顶点,∴(不妨设)A(﹣a,0),B(a,0).
的公共顶点,∴(不妨设)A(﹣a,0),B(a,0).
设P(x1,y1),M(x2,y2),∵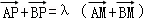 ,其中λ∈R,∴(x1+a,y1)+(x1﹣a,y1)=λ[(x2+a,y2)+(x2﹣a,y2)],化为x1y2=x2y1.
,其中λ∈R,∴(x1+a,y1)+(x1﹣a,y1)=λ[(x2+a,y2)+(x2﹣a,y2)],化为x1y2=x2y1.
∵P、M都异于A、B,∴y1≠0,y2≠0.∴ .
.
由k1+k2=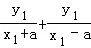 =5,化为
=5,化为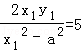 ,(*)
,(*)
又∵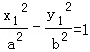 ,∴
,∴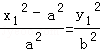 ,代入(*)化为
,代入(*)化为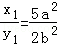 .
.
k3+k4=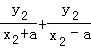 =
=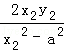 ,又
,又 ,
,
∴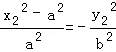 ,
,
∴k3+k4=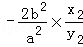 =
=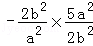 =﹣5.
=﹣5.
故答案为﹣5.
考点:双曲线和椭圆的方程
点评:熟练掌握点在曲线上的意义、双曲线和椭圆的方程、向量的运算性质、斜率的计算公式是解题的关键,同时本题需要较强的计算能力


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com