Question

【题目】无线电技术在航海中有很广泛的应用，无线电波可以作为各种信息的载体．现有一艘航行中的轮船需要与陆地上的基站进行通信，其连续向基站拍发若干次呼叫信号，每次呼叫信号被基站收到的概率都是0.2，基站收到呼叫信号后立即向轮船拍发回答信号，回答信号一定能被轮船收到．

（Ⅰ）若要保证基站收到信号的概率大于0.99，求轮船至少要拍发多少次呼叫信号．

（Ⅱ）设（Ⅰ）中求得的结果为．若轮船第一次拍发呼叫信号后，每隔5秒钟拍发下一次，直到收到回答信号为止，已知该轮船最多拍发次呼叫信号，且无线电信号在轮船与基站之间一个来回需要16秒，设轮船停止拍发时，一共拍发了次呼叫信号，求的数学期望（结果精确到0.01）．

参考数据：．

Answer 1

【答案】（Ⅰ）21次（Ⅱ）7.91

【解析】

（Ⅰ）设“轮船拍发次呼叫信号，基站至少收到1次信号”为事件，则，因而可知其对立事件满足，根据独立事件概率公式即可得及的值，即可做出判断.

（Ⅱ）由（Ⅰ）可知，根据拍发间隔时间及信号在轮船与基站之间一个来回时间可得停止拍发时轮船一共拍发了次呼叫信号，进而可得随机变量的分布列，根据数学期望公式，结合错位相减法即可得解.

（1）设“轮船拍发次呼叫信号，基站至少收到1次信号”为事件，则其对立事件表示“轮船拍发次呼叫信号，基站收到0次信号”，其中为正整数．

要使，则需．

由题可知．

因为，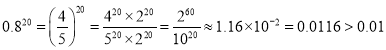

而，

又因为，所以，即轮船至少要拍发21次呼叫信号．

（Ⅱ）若第1次呼叫信号就被基站收到，则轮船16秒后会收到回答信号从而停止拍发，16秒内轮船会继续拍发3次，即一共拍发了4次呼叫信号；

若前次呼叫信号都没有被基站收到，第次呼叫信号被基站收到，与上面同理，停止拍发时轮船一共拍发了次呼叫信号；

若前17次呼叫信号都没有被基站收到，轮船会拍发21次后停止，

所以随机变量的分布列如下：

	4	5	6	…	19	20	21
	0.2			…

所以

，

所以．

，

两式相减得

所以．