
分析 (1)利用函数单调性的定义进行证明即可.
(2)根据函数奇偶性和单调性的关系将不等式进行转化进行求解即可.
解答 (1)证明:在区间[0,2]上任取x1,x2且x1<x2
f(x1)-f(x2)=x12+4x1+1-(x22+4x2+1)=(x1-x2)(x1+x2+4),
∵0≤x1<x2≤2,
∴x1-x2<0,x1+x2+4>0,
∴f(x1)-f(x2)<0,
即∴f(x1)<f(x2),
∴f(x)在[0,2]上是增函数.(4分)
(2)由已知:f(|x|)>f(|1-x|),
∴$\left\{{\begin{array}{l}{-2≤x≤2}\\{-2≤1-x≤2}\\{|x|>|1-x|}\end{array}}\right.$
解得$\frac{1}{2}<x≤2$
∴不等式的解集为$({\frac{1}{2},2}]$(8分)
点评 本题主要考查函数单调性的判断,以及不等式的求解,利用定义法结合函数单调性的定义是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 503 | B. | $\frac{1007}{2}$ | C. | 1006 | D. | 1007 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
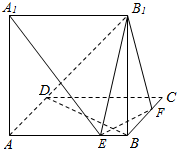 如图,正方形ABCD所在平面与正方形ABB1A1所在的平面垂直,且AB等于1.设E、F分别为AB、BC上的动点,(不包括端点)
如图,正方形ABCD所在平面与正方形ABB1A1所在的平面垂直,且AB等于1.设E、F分别为AB、BC上的动点,(不包括端点)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13+20×13×1% | B. | 13+21×13×1% | C. | 13×(1+1%)20 | D. | 13×(1+1%)21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com