
分析 欲判断集合M、N的关系,先对集合N中的整数k分奇偶进行讨论,再根据集合的包含关系即可得这两个数集的关系.
解答 解:M={x|x=$\frac{k}{2}$+$\frac{1}{4}$=$\frac{2k+1}{4}$,k∈Z},显然M的分子为奇数,
N={x|x=$\frac{k}{4}$+$\frac{1}{2}$=$\frac{k+2}{4}$,k∈Z},显然N的分子为整数,
∴集合M、N的关系为M?N.∵x0∈M,∴x0∈N
故答案为x0∈N.
点评 本题主要考查集合的包含关系判断及应用等基本运算,属于基础题.要正确判断两个集合间包含的关系,必须对集合的相关概念有深刻的理解,善于抓住代表元素,认清集合的特征.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | x+y-3=0 | B. | x+y+b-a=0 | C. | x+y-a-b=0 | D. | x-y+3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
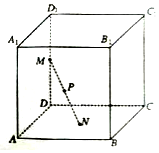 如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,长为1的线段MN的一个端点M在棱DD1上运动,点N在正方形ABCD内运动,则MN中点P的轨迹的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值8 | B. | 最小值10 | C. | 最大值12 | D. | 最小值14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{3}}]$ | B. | $({1,\sqrt{2}}]$ | C. | $[{\sqrt{3},+∞})$ | D. | $[{\sqrt{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,且$\overrightarrow{a}$与$\overrightarrow{b}$同向,则$\overrightarrow{a}$>$\overrightarrow{b}$ | B. | 当实数λ=0时,λ$\overrightarrow{a}$=0 | ||
| C. | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | D. | |$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com