
设函数
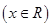 满足
满足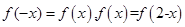 ,且当
,且当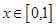 时,
时,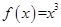 .又函数
.又函数 ,则函数
,则函数 在
在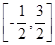 上的零点个数为( )
上的零点个数为( )
A.5 B.6 C.7 D.8
B
【解析】
试题分析:在同一坐标系内画出函数y=f(x)和y=g(x)的图象,在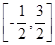 上
上
图象交点的个数既是h(x)零点的个数。
∵f(-x)=f(x),∴f(x)是偶函数
∵f(x)=f(2-x)
∴f(-x+2)=f(-x)
∴f(x)=f(x+2)
∴f(x)是周期函数,周期为2
∵当x∈[0,1]时,f(x)=x³
∴当x∈[-1,0]]时,f(x)=-x³
∴x∈[1,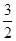 ]时,f(x)=f(x-2)=-(x-2)³
]时,f(x)=f(x-2)=-(x-2)³
g(x)=|xcos(πx)|
g(-x)=g(x),g(x)是偶函数
x∈[-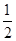 ,
,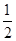 ], πx∈[-
], πx∈[-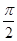 ,
,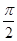 ],cosπx>0
],cosπx>0
g(x)=xcos(πx), g'(x)=cos(πx)-πsin(πx)=0
x∈[1,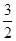 ],πx∈[π,
],πx∈[π,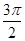 ],cosπx<0
],cosπx<0
g(x)=-xcos(πx)
可在同一坐标系内画出函数在[-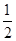 ,
,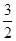 ]上的简图,观察交点个数为6个,
]上的简图,观察交点个数为6个,
∴h(x)=g(x)-f(x)在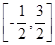 上的零点个数有6个,选B.
上的零点个数有6个,选B.
考点:本题主要考查函数零点的概念,函数的图象和性质,函数的奇偶性、周期性。
点评:难题,通过分析函数特征,明确了函数图象的大致形态,在同一坐标系内观察两图象的交点情况。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011年湖南省普通高等学校招生统一考试文科数学 题型:填空题
给定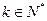 ,设函数
,设函数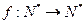 满足:对于任意大于
满足:对于任意大于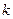 的正整数
的正整数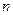 ,
,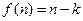
(1)设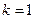 ,则其中一个函数
,则其中一个函数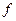 在
在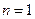 处的函数值为 ;
处的函数值为 ;
(2)设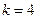 ,且当
,且当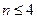 时,
时,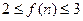 ,则不同的函数
,则不同的函数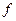 的个数为 。
的个数为 。
查看答案和解析>>
科目:高中数学 来源:2014届云南省高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
设函数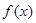 满足
满足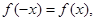 且当
且当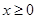 时,
时,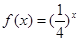 ,又函数
,又函数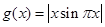 ,则函数
,则函数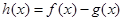 在
在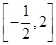 上的零点个数为 (
)
上的零点个数为 (
)
(A)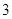 (B)
(B)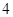 (C)
(C)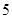 (D)
(D)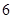
查看答案和解析>>
科目:高中数学 来源:2015届福建省、二中高一上学期期末联考数学卷(解析版) 题型:选择题
设函数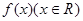 满足
满足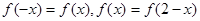 ,且当
,且当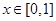 时,
时,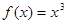 .又函数
.又函数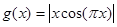 ,则函数
,则函数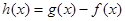 在
在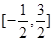 上的零点个数为
( )
上的零点个数为
( )
A.5 B. 6 C.7 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com