
分析 (Ⅰ)求出抛物线C:x2=4y的焦点F(0,1)设A(x1,y1),B(x2,y2),联立x2=4y与y=kx+a有x2-4kx-4a=0,则△=16(k2+a)>0,且x1+x2=4k,x1•x2=-4a,求出导函数$y'=\frac{1}{2}x$利用切线方程,结合韦达定理,化简求解即可.
(Ⅱ)若直线l过焦点F,则a=1,则x1+x2=4k,x1•x2=-4.求出圆x2+(y-1)2=1圆心为F(0,1),半径为1,由抛物线的定义有|AF|=y1+1,|BF|=y2+1,吐槽|AD|=|AF|-1=y1,|BE|=|BF|-1=y2,利用|AD|•|BE|=y1y2,转化求解|AD|•|BE|为定值.
解答 解:抛物线C:x2=4y的焦点F(0,1),…(1分)
设A(x1,y1),B(x2,y2),联立x2=4y与y=kx+a有x2-4kx-4a=0,
则△=16(k2+a)>0,且x1+x2=4k,x1•x2=-4a.…(2分)
(Ⅰ)由x2=4y有$y=\frac{1}{4}{x^2}$,则$y'=\frac{1}{2}x$,…(3分)
则抛物线C在$A({{x_1},\frac{1}{4}x_1^2})$处的切线为$y-\frac{1}{4}x_1^2=\frac{1}{2}{x_1}({x-{x_1}})$,
即$y=\frac{1}{2}{x_1}x-\frac{1}{4}x_1^2$…①…(4分)
同理抛物线C在$B({{x_2},\frac{1}{4}x_2^2})$处的切线为$y=\frac{1}{2}{x_2}x-\frac{1}{4}x_2^2$…②…(5分)
联立①②解得$x=\frac{{{x_1}+{x_2}}}{2}$,代入①式解得$y=\frac{{{x_1}{x_2}}}{4}=-a$,
即P(2k,-a).…(6分)
(Ⅱ)若直线l过焦点F,则a=1,则x1+x2=4k,x1•x2=-4.
由条件可知圆x2+(y-1)2=1圆心为F(0,1),半径为1,…(7分)
由抛物线的定义有|AF|=y1+1,|BF|=y2+1,…(8分)
则|AD|=|AF|-1=y1,|BE|=|BF|-1=y2,…10分,
|AD|•|BE|=y1y2=(kx1+1)(kx2+1)
=${k^2}{x_1}{x_2}+k({{x_1}+{x_2}})+1=-4{k^2}+4{k^2}+1=1$,
(或$|{AD}|•|{BE}|={y_1}{y_2}=\frac{x_1^2}{4}•\frac{x_1^2}{4}=\frac{{{{({{x_1}{x_2}})}^2}}}{16}=\frac{{{{({-4})}^2}}}{16}=1$)
即|AD|•|BE|为定值,定值为1.…(12分)
点评 本题考查导数的应用,抛物线与直线的位置关系的综合应用,考查转化思想以及计算能力.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | x+2y-3=0 | B. | x+4y-5=0 | C. | 4x+y-5=0 | D. | x-2y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
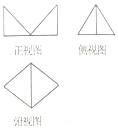 某几何体的三视图如图所示,其侧视图是一个边长为2的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为2,表面积为2$\sqrt{6}$+6$\sqrt{3}$.
某几何体的三视图如图所示,其侧视图是一个边长为2的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为2,表面积为2$\sqrt{6}$+6$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 非p或q | B. | p且q | C. | 非p且非q | D. | 非p或非q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
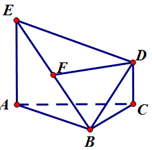 如图,△ABC为等边三角形,EA⊥平面ABC,EA∥DC,EA=2DC,F为EB的中点.
如图,△ABC为等边三角形,EA⊥平面ABC,EA∥DC,EA=2DC,F为EB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com