
分析 由an+1=2an+1,n∈N*,变形为an+1+1=2(an+1),利用等比数列的通项公式即可得出.于是C${\;}_{n}^{1}$a1+C${\;}_{n}^{2}$a2+…+C${\;}_{n}^{n}$an=C${\;}_{n}^{1}$×2+C${\;}_{n}^{2}$×22+…+C${\;}_{n}^{n}$2n-(C${\;}_{n}^{1}$+C${\;}_{n}^{2}$+…+C${\;}_{n}^{n}$),再利用二项式定理即可得出.
解答 解:由an+1=2an+1,n∈N*,
∴an+1+1=2(an+1),
∴数列{an+1}为等比数列,首项为2,公比为2,
∴an+1=2n,
∴an=2n-1.
∴C${\;}_{n}^{1}$a1+C${\;}_{n}^{2}$a2+…+C${\;}_{n}^{n}$an=C${\;}_{n}^{1}$×2+C${\;}_{n}^{2}$×22+…+C${\;}_{n}^{n}$2n-(C${\;}_{n}^{1}$+C${\;}_{n}^{2}$+…+C${\;}_{n}^{n}$)
=(1+2)n-1-2n+1
=3n-2n.
故答案为:3n-2n.
点评 本题考查了等比数列的通项公式、二项式定理,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
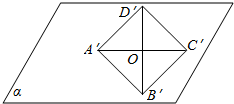 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.
在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com