
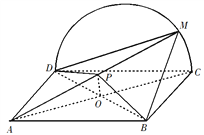
【题目】如图,矩形![]() 所在平面与半圆弧
所在平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?说明理由.
?说明理由.

【答案】(1)证明见解析
(2)存在,理由见解析
【解析】分析:(1)先证![]() ,再证
,再证![]() ,进而完成证明。
,进而完成证明。
(2)判断出P为AM中点,,证明MC∥OP,然后进行证明即可。
详解:(1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC![]() 平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
因为M为![]() 上异于C,D的点,且DC为直径,所以DM⊥CM.
上异于C,D的点,且DC为直径,所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM![]() 平面AMD,故平面AMD⊥平面BMC.
平面AMD,故平面AMD⊥平面BMC.
(2)当P为AM的中点时,MC∥平面PBD.
证明如下:连结AC交BD于O.因为ABCD为矩形,所以O为AC中点.
连结OP,因为P为AM 中点,所以MC∥OP.
MC![]() 平面PBD,OP
平面PBD,OP![]() 平面PBD,所以MC∥平面PBD.
平面PBD,所以MC∥平面PBD.


科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
①从1,2,3,4,5中任取2个不同的数,事件![]() “取到的2个数之和为偶数”,事件
“取到的2个数之和为偶数”,事件![]() “取到的
“取到的
2个数均为偶数”,则![]() ;
;
②某班共有45名学生,其中30名男同学,15名女同学,老师随机抽查了5名同学的作业,用![]() 表示抽查到的女生的人数,则
表示抽查到的女生的人数,则![]() ;
;
③设随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
④由直线![]() ,
,![]() ,曲线
,曲线![]() 及
及![]() 轴所围成的图形的面积是
轴所围成的图形的面积是![]() .
.
其中所有正确结论的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是椭圆上一点.
是椭圆上一点.
(1)求椭圆的标准方程;
(2)过椭圆右焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,
两点,![]() 是直线
是直线![]() 上任意一点.
上任意一点.
证明:直线![]() 的斜率成等差数列.
的斜率成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. 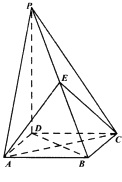
(1)求证:平面AEC⊥平面PDB;
(2)当PD=2AB,且E为PB的中点,求二面角B﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”,若
的“不动点”,若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”,函数
的“稳定点”,函数![]() 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为![]() 和
和![]() ,即
,即![]() ,
,![]() ,那么,
,那么,
(1)求函数![]() 的“稳定点”;
的“稳定点”;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,将
,将![]() 的图象向右平移两个单位长度,得到函数
的图象向右平移两个单位长度,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且仅有一个实根,求
上有且仅有一个实根,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,设
对称,设![]() ,已知
,已知![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com