
【题目】已知椭圆![]()
![]() 长轴长为短轴长的两倍,连结椭圆的四个顶点得到的菱形的面积为4,直线
长轴长为短轴长的两倍,连结椭圆的四个顶点得到的菱形的面积为4,直线![]() 过点
过点![]() ,且与椭圆相交于另一点
,且与椭圆相交于另一点![]() .
.
(1)求椭圆的方程;
(2)若线段![]() 长为
长为![]() ,求直线
,求直线![]() 的倾斜角;
的倾斜角;
(3)点![]() 在线段
在线段![]() 的垂直平分线上,且
的垂直平分线上,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)由椭圆![]() 长轴长为短轴长的两倍,连接椭圆的四个顶点得到的菱形的面积为4,列出方程组求出
长轴长为短轴长的两倍,连接椭圆的四个顶点得到的菱形的面积为4,列出方程组求出![]() ,
,![]() ,即可求椭圆的方程;
,即可求椭圆的方程;
(2)直线![]() 的方程代入椭圆方程,利用韦达定理,结合弦长公式,即可求得结论.
的方程代入椭圆方程,利用韦达定理,结合弦长公式,即可求得结论.
(3)设直线![]() 的方程为
的方程为![]() ,由
,由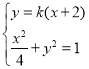 ,得
,得![]() ,由此根据
,由此根据![]() 和
和![]() 两种情况分类讨论经,能求出结果.
两种情况分类讨论经,能求出结果.
解:(1)![]() 椭圆
椭圆![]() 长轴长为短轴长的两倍,
长轴长为短轴长的两倍,
连结椭圆的四个顶点得到的菱形的面积为4,
![]()
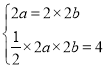 ,
,
解得![]() ,
,![]() .
.
所以椭圆的方程为![]() .
.
(2)由(1)可知点![]() 的坐标是
的坐标是![]() .
.
设点![]() 的坐标为
的坐标为![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
代入椭圆方程,消去![]() 并整理,得
并整理,得![]() .
.
由![]() ,得
,得![]() .
.
从而![]() .
.
所以![]() .
.
由![]() ,得
,得![]() .
.
整理得![]() ,即
,即![]() ,解得
,解得![]() .
.
所以直线![]() 的倾斜角
的倾斜角![]() 或
或![]() .
.
(3)由(1)可知![]() .设
.设![]() 点的坐标为
点的坐标为![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
于是![]() ,
,![]() 两点的坐标满足方程组
两点的坐标满足方程组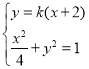 ,
,
由方程组消去![]() 并整理,得
并整理,得![]() ,
,
由![]() ,得
,得![]() ,从而
,从而![]() ,
,
设线段![]() 是中点为
是中点为![]() ,则
,则![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
以下分两种情况:
①当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .线段
.线段![]() 的垂直平分线为
的垂直平分线为![]() 轴,于是
轴,于是
![]() ,
,![]() ,由
,由![]() ,得
,得![]() ;
;
②当![]() 时,线段
时,线段![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,
,
令![]() ,解得
,解得![]() ,
,
由![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
整理得![]() ,故
,故![]() ,解得
,解得![]() .
.
综上![]() 或
或![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,且Sn=n(n+1)(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)令![]() (n∈N*),求数列{cn}的前n项和Tn.
(n∈N*),求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学随机抽取部分高一学生调查其每日自主安排学习的时间(单位:分钟),并将所得数据绘制成如图所示的频率分布直方图,其中自主安排学习时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
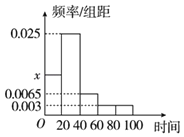
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)从学校全体高一学生中任选![]() 名学生,这
名学生,这![]() 名学生中自主安排学习时间少于
名学生中自主安排学习时间少于![]() 分钟的人数记为
分钟的人数记为![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率).
的分布列和数学期望.(以直方图中的频率作为概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为![]() ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
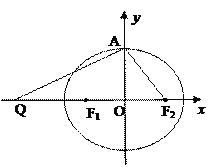
【题目】如图,设椭圆![]() 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且![]() 0,若过 A,Q,F2三点的圆恰好与直线
0,若过 A,Q,F2三点的圆恰好与直线![]() 相切,过定点 M(0,2)的直线
相切,过定点 M(0,2)的直线![]() 与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线
与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线![]() 的斜率
的斜率![]() ,在x轴上是否存在点P(
,在x轴上是否存在点P(![]() ,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出
,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,请说明理由;(Ⅲ)若实数
的取值范围;如果不存在,请说明理由;(Ⅲ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3个红球与3个黑球随机排成一行,从左到右依次在球上标记1,2,3,4,5,6,则红球上的数字之和小于黑球上的数字之和的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 为正方形,
为正方形,![]() 平面
平面![]() ,四边形
,四边形![]() 与四边形
与四边形![]() 也都为正方形,连接
也都为正方形,连接![]() ,点
,点![]() 为
为![]() 的中点,有下述四个结论:
的中点,有下述四个结论:
①![]() ; ②
; ②![]() 与
与![]() 所成角为
所成角为![]() ;
;
③![]() 平面
平面![]() ; ④
; ④![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com