
���� ��1������C����������ȥ�����ȣ����������C�ķ��̣��ɦ�cos��=x����sin��=y�������ֱ��l��ֱ�����귽�̣�
��2��������C�ϵĵ�Ϊ��$\sqrt{3}cos��$��sin�ȣ������õ㵽ֱ�ߵľ��빫ʽ���������C�ϵĵ㵽ֱ��l�ľ�������ֵ��
��� �⣺��1������C��������Ϊ$\left\{\begin{array}{l}{x=\sqrt{3}cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������
��ȥ�����ȣ�������C�ķ���Ϊ$\frac{x^2}{3}+{y^2}=1$��
ֱ��l�ļ����귽��Ϊ��cos����-$\frac{��}{4}$��=2$\sqrt{2}$��
��$�ѣ�cos��cos\frac{��}{4}+sin��sin\frac{��}{4}��$=2$\sqrt{2}$��
�������æ�cos��+��sin��=4��
�ߦ�cos��=x����sin��=y��
ֱ��l��ֱ�����귽��Ϊx+y-4=0��
��2��������C�ϵĵ�Ϊ��$\sqrt{3}cos��$��sin�ȣ���
������C�ϵĵ㵽ֱ��l�ľ��룺
$d=\frac{{|{\sqrt{3}cos��+sin��-4}|}}{{\sqrt{2}}}=\frac{{|{2sin����+\frac{��}{3}��-4}|}}{{\sqrt{2}}}��3\sqrt{2}$��
������C�ϵĵ㵽ֱ��l�ľ�������ֵ${d_{max}}=3\sqrt{2}$��
���� ���⿼�����ߵ���ͨ���̺�ֱ�ߵ�ֱ�����귽�̵������������ϵĵ㵽ֱ��l�ľ�������ֵ�������鼫���ꡢֱ������Ļ���������������֤�����������������������ת������˼�롢���ν��˼�룬���е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015-2016ѧ�꼪��ʡ��һ��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪�����Ϊ����������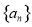 ����ǰn���Ϊ
����ǰn���Ϊ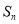 ����
���� �ɵȲ����У�������
�ɵȲ����У�������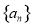 ��ͨ�ʽΪ�� ��
��ͨ�ʽΪ�� ��
A��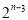 B��
B��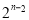 C��
C��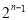 D��
D��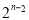 +1
+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��С������Ϊ�е��溯�� | B�� | ��С������Ϊ�е�ż���� | ||
| C�� | ��С������Ϊ$\frac{��}{2}$���溯�� | D�� | ��С������Ϊ$\frac{��}{2}$��ż���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x-y-5=0 | B�� | x-3y+9=0 | C�� | 3x+y-13=0 | D�� | x+3y-15=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | $S=\frac{100}{101}��P=\frac{100}{101}$ | B�� | $S=\frac{99}{100}��P=\frac{99}{202}$ | ||
| C�� | $S=\frac{100}{101}��P=\frac{99}{202}$ | D�� | $S=\frac{100}{101}��P=\frac{99}{100}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com