
给出下列四个命题,其错误的是( )
①已知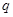 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 是递增数列”是“
是递增数列”是“ ”的既不充分也不必要条件;
”的既不充分也不必要条件;
②若定义在 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
;
③若存在正常数 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
;
④函数 与
与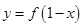 图像关于
图像关于 对称.
对称.
A.②④ B.④ C.③ D.③④
B
【解析】
试题分析:对于命题①,如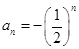 ,数列
,数列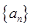 是递增的等比数列,但此时等比数列
是递增的等比数列,但此时等比数列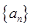 的公比
的公比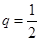 ,另一方面,若等比数列
,另一方面,若等比数列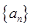 的每一项均为负数,即对任意
的每一项均为负数,即对任意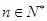 ,有
,有 ,
,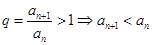 ,即等比数列
,即等比数列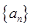 为递减数列,故“数列
为递减数列,故“数列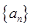 是递增数列”是“
是递增数列”是“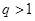 ”的既不充分也不必要条件,即命题①正确;对于命题②,由于函数
”的既不充分也不必要条件,即命题①正确;对于命题②,由于函数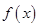 是
是 上的奇函数,则有
上的奇函数,则有 ,故对于任意的实数
,故对于任意的实数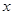 ,均有
,均有 ,故命题②正确;对于命题③,令
,故命题②正确;对于命题③,令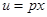 ,则有
,则有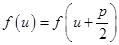 ,故
,故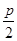 是函数
是函数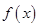 的一个周期,故命题③正确;对于命题④,设点
的一个周期,故命题③正确;对于命题④,设点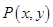 在函数
在函数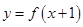 上,则有
上,则有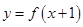 ,另一方面,
,另一方面, ,则点
,则点 在函数
在函数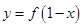 的图象上,而点
的图象上,而点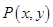 与点
与点 关于
关于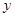 轴对称,即函数
轴对称,即函数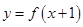 与
与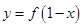 图像关于
图像关于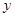 轴对称,故命题④错误,故选B.
轴对称,故命题④错误,故选B.
考点:1.充分必要条件;2.函数的奇偶性;3.函数的周期性;4.函数图象的对称性;5.命题真假性的判断


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
| 8 |
| 9 |
| 7 |
| 6 |
| 1 |
| 3 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com