
甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为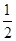 、
、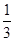 、
、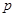 ,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为
,且他们是否破译出密码互不影响,若三人中只有甲破译出密码的概率为 .
.
(1)求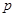 的值.
的值.
(2)设甲、乙、丙三人中破译出密码的人数为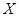 ,求
,求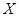 的分布列和数学期望
的分布列和数学期望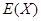 .
.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
考察某种药物预防甲型H1N1流感的效果,进行动物试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(Ⅰ)根据所给样本数据完成下面2×2列联表;
(Ⅱ)请问能有多大把握认为药物有效?
| | 不得流感 | 得流感 | 总计 |
| 服药 | | | |
| 不服药 | | | |
| 总计 | | | |
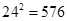 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表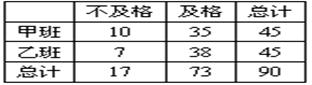
根据表中数据,你有多大把握认为成绩及格与班级有关?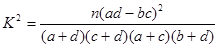
附表:
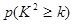 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是一个从 的”闯关”游戏.
的”闯关”游戏. 
规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于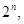 则闯关成功.
则闯关成功.
(1)求闯第一关成功的概率;
(2)记闯关成功的关数为随机变量X,求X的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年4月20日8时02分四川省雅安市芦山县(北纬30.3,东经103.0)发生7.0级地震。一方有难,八方支援,重庆众多医务工作者和志愿者加入了抗灾救援行动。其中重庆某医院外科派出由5名骨干医生组成的救援小组,奔赴受灾第一线参与救援。现将这5名医生分别随机分配到受灾最严重的芦山、宝山、天全三县中的某一个。
(1)求每个县至少分配到一名医生的概率。
(2)若将随机分配到芦山县的人数记为 ,求随机变量
,求随机变量 的分布列,期望和方差。
的分布列,期望和方差。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店试销某种商品,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 概率 | 0.05 | 0.25 | 0.45 | 0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知甲箱中只放有x个红球与y个白球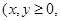 且
且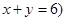 ,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
,乙箱中只放有2个红球、1个白球与1个黑球(球除颜色外,无其它区别). 若甲箱从中任取2个球, 从乙箱中任取1个球.
(Ⅰ)记取出的3个球的颜色全不相同的概率为P,求当P取得最大值时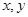 的值;
的值;
(Ⅱ)当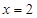 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数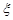 的期望
的期望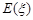 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作。规定:至少正确完成其中2题的便可提交通过。已知6道备选题中考生甲有4道题能正确完成,2道题不能完成。
(1)求出甲考生正确完成题数的概率分布列,并计算数学期望;
(2)若考生乙每题正确完成的概率都是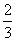 ,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为提高学生的素质,学校决定开设一批选修课程,分别为“文学”、“艺术”、“竞赛”三类,这三类课程所含科目的个数分别占总数的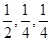 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求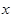 的分布列及期望。
的分布列及期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com