
分析 由题意,图形关于x轴对称,A,B,P三点共线,可得$\frac{{y}_{1}}{{x}_{1}+1}$=$\frac{{y}_{2}}{{x}_{2}+1}$.由焦半径公式|AF|=x1+1=|NF|,||BF|=x2+1=|MF|,$\frac{|AF|}{|FM|}$+$\frac{|BF|}{|FN|}$=$\frac{{y}_{1}}{{y}_{2}}$+$\frac{{y}_{2}}{{y}_{1}}$=18,(y1+y2)2=20y1y2,再利用韦达定理,即可得出结论.
解答 解:由题意,图形关于x轴对称,A,B,P三点共线,可得$\frac{{y}_{1}}{{x}_{1}+1}$=$\frac{{y}_{2}}{{x}_{2}+1}$.
由焦半径公式|AF|=x1+1=|NF|,||BF|=x2+1=|MF|,
∴$\frac{|AF|}{|FM|}$+$\frac{|BF|}{|FN|}$=$\frac{{y}_{1}}{{y}_{2}}$+$\frac{{y}_{2}}{{y}_{1}}$=18,∴(y1+y2)2=20y1y2,
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=k(x+1)}\end{array}\right.$,可得ky2-4y+4k=0,
∴y1+y2=$\frac{4}{k}$,y1y2=4,∴$\frac{16}{{k}^{2}}$=80,
∵k>0,∴k=$\frac{\sqrt{5}}{5}$.
故答案为$\frac{\sqrt{5}}{5}$.
点评 本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
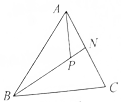 如图,在△ABC中,已知$\overrightarrow{AN}$=$\frac{1}{2}\overrightarrow{AC}$,P是BN上一点,若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,则实数m的值是$\frac{1}{2}$.
如图,在△ABC中,已知$\overrightarrow{AN}$=$\frac{1}{2}\overrightarrow{AC}$,P是BN上一点,若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,则实数m的值是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com