
如图,直线AB为圆O的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.

(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
(1)见解析 (2) 
【解析】
(1)证明 连接DE,则∠DCB=∠DEB,

∵DB⊥BE,
∴∠DBC+∠CBE=90°,∠DEB+∠EDB=90°,
∴∠DBC+∠CBE=∠DEB+∠EDB,
又∠CBE=∠EBF=∠EDB,
∴∠DBC=∠DEB=∠DCB,
∴DB=DC.
(2)解 由(1)知:∠CBE=∠EBF=∠BCE,

∴∠BDE=∠CDE,
∴DE是BC的垂直平分线,
设交点为H,则BH= ,
,
∴OH=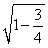 =
= ,
,
∴DH= ,
,
∴tan∠BDE= =
= ,
,
∴∠BDE=30°,
∴∠FBE=∠BDE=30°,
∴∠CBF+∠BCF=90°,
∴∠BFC=90°,
∴BC是△BCF的外接圆直径.
∴△BCF的外接圆半径为


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用4练习卷(解析版) 题型:填空题
已知函数f(x)=aln x+x在区间[2,3]上单调递增,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用2练习卷(解析版) 题型:填空题
一块形状为直角三角形的铁皮,两直角边长分别为40 cm、60 cm,现要将它剪成一个矩形,并以此三角形的直角为矩形的一个角,则矩形的最大面积是________cm2.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用22练习卷(解析版) 题型:解答题
如图,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2),圆O1的弦AB交圆O2于点C(O1不在AB上).

求证:AB∶AC为定值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用21练习卷(解析版) 题型:填空题
袋中装有大小相同且形状一样的四个球,四个球上分别标有“2”、“3”、“4”、“6”这四个数.现从中随机选取三个球,则所选的三个球上的数恰好能构成一个等差数列的概率是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用20练习卷(解析版) 题型:填空题
设l,m是两条不同的直线,α是一个平面,有下列四个命题:
①若l⊥α,m?α,则l⊥m;②若l⊥α,l∥m,则m⊥α;
③若l∥α,m?α,则l∥m;④若l∥α,m∥α,则l∥m.
则其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用15练习卷(解析版) 题型:解答题
在平面直角坐标系xOy中,求过椭圆 (φ为参数)的右焦点,且与直线
(φ为参数)的右焦点,且与直线 (t为参数)平行的直线的普通方程.
(t为参数)平行的直线的普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com