
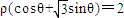 的距离为d,求d的最大值.
的距离为d,求d的最大值.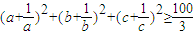 .
.
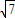 ,最后利用△AED∽△BEC,由对应边成比例得到BC=2AD=2
,最后利用△AED∽△BEC,由对应边成比例得到BC=2AD=2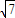 .
.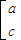 ,利用矩阵乘法的法则,结合题意列出关于a、b、c、d的方程组并解之,可得矩阵M,再用二阶矩阵逆矩阵的公式,可算出矩阵M的逆矩阵M-1;
,利用矩阵乘法的法则,结合题意列出关于a、b、c、d的方程组并解之,可得矩阵M,再用二阶矩阵逆矩阵的公式,可算出矩阵M的逆矩阵M-1;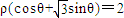 的普通方程为
的普通方程为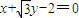 .设圆上的点A(3cosα,3sinα),利用点到直线的距离公式结合正弦函数的最值,可算出圆上的点到直线距离的最大值.
.设圆上的点A(3cosα,3sinα),利用点到直线的距离公式结合正弦函数的最值,可算出圆上的点到直线距离的最大值.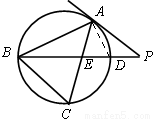
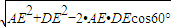 =
=
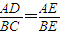 =
= ,可得
,可得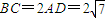
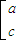 ,则有
,则有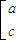
 =
= ,
,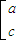
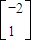 =
=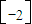 ,
, ,且
,且 ,解得
,解得
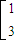 ,从而M-1=
,从而M-1=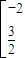
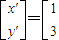 ,所以
,所以
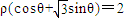 可化为
可化为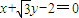
 =
=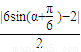 ,
,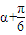 )=-1时,d的最大值为4.
)=-1时,d的最大值为4.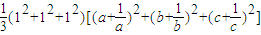
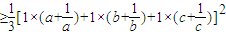 =
=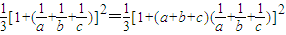
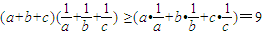
 ,即不等式
,即不等式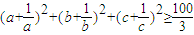 成立.
成立.

科目:高中数学 来源: 题型:
|
| a |
|
|
| x2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•江苏二模)选做题
(2012•江苏二模)选做题| PC |
| PA |
| BD |
| DC |
|
| x2 |
| 16 |
| y2 |
| 9 |
| 13 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 [选做题]
[选做题]| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 100 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com