练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4、若函数f（x）=kax-a-x（a＞0且a≠1）既是奇函数，又是增函数，那么g（x）=loga（x+k） 的图象是（　　）
    分析：由函数f（x）=kax-a-x，（a＞0，a≠1）在（-∞，+∞）上既是奇函数，又是增函数，则由复合函数的性质，我们可得k=1，a＞1，由此不难判断函数的图象．
    解答：解：∵函数f（x）=kax-a-x，（a＞0，a≠1）在（-∞，+∞）上是奇函数
    则f（-x）+f（x）=0
    即（k-1）ax-a-x=0
    则k=1
    又∵函数f（x）=kax-a-x，（a＞0，a≠1）在（-∞，+∞）上是增函数
    则a＞1
    则g（x）=loga（x+k）=loga（x+1）
    函数图象必过原点，且为增函数
    故选D
    点评：若函数在其定义域为为奇函数，则f（-x）+f（x）=0，若函数在其定义域为为偶函数，则f（-x）-f（x）=0，这是函数奇偶性定义的变形使用，另外函数单调性的性质，在公共单调区间上：增函数-减函数=增函数也是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    对于具有相同定义域D的函数f（x）和g（x），若存在函数h（x）=kx+b（k，b为常数）对任给的正数m，
    存在相应的x0∈D使得当x∈D且x＞x0时，总有
    0＜f(x)-h(x)＜m
    0＜h(x)-g(x)＜m
    ，则称直线l：y=ka+b为曲线y=f（x）和y=g（x）的“分渐进性”．给出定义域均为D={x|x＞1}的四组函数如下：
    ①f（x）=x2，g（x）=
    		x
    ②f（x）=10-x+2，g（x）=
    2x-3
    x
    ③f（x）=
    x2+1
    x
    ，g（x）=
    xlnx+1
    lnx
    ④f（x）=
    2x2
    x+1
    ，g（x）=2（x-1-e-x）
    其中，曲线y=f（x）和y=g（x）存在“分渐近线”的是（　　）
    A、①④B、②③C、②④D、③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    集合C={f（x）|f（x）是在其定义域上的单调增函数或单调减函数}，集合D={f（x）|f（x）在定义域内存在区间[a，b]，使得f（x）在a，b上的值域是[ka，kb]，k为常数}．
    （1）当k=
    1
    2
    时，判断函数f（x）=
    		x
    是否属于集合C∩D？并说明理由．若是，则求出区间[a，b]；
    （2）当k=
    1
    2
    0时，若函数f（x）=
    		x
    +t∈C∩D，求实数t的取值范围；
    （3）当k=1时，是否存在实数m，当a+b≤2时，使函数f（x）=x2-2x+m∈D，若存在，求出m的范围，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：江苏期中题 题型：解答题

    函数f（x）=ka﹣x（k，a为常数，a＞0且a≠1）的图象过点A（0，1），B（3，8）．
    （1）求函数f（x）的解析式；
    （2）若函数，试判断函数g（x）的奇偶性．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    集合C={f（x）|f（x）是在其定义域上的单调增函数或单调减函数}，集合D={f（x）|f（x）在定义域内存在区间[a，b]，使得f（x）在a，b上的值域是[ka，kb]，k为常数}．
    （1）当k=
    1
    2
    时，判断函数f（x）=
    		x
    是否属于集合C∩D？并说明理由．若是，则求出区间[a，b]；
    （2）当k=
    1
    2
    0时，若函数f（x）=
    		x
    +t∈C∩D，求实数t的取值范围；
    （3）当k=1时，是否存在实数m，当a+b≤2时，使函数f（x）=x2-2x+m∈D，若存在，求出m的范围，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省绍兴一中高一（上）段考数学试卷（解析版） 题型：解答题

    集合C={f（x）|f（x）是在其定义域上的单调增函数或单调减函数}，集合D={f（x）|f（x）在定义域内存在区间[a，b]，使得f（x）在a，b上的值域是[ka，kb]，k为常数}．
    （1）当k=时，判断函数f（x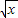）=是否属于集合C∩D？并说明理由．若是，则求出区间[a，b]；
    （2）当k=0时，若函数f（x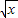）=+t∈C∩D，求实数t的取值范围；
    （3）当k=1时，是否存在实数m，当a+b≤2时，使函数f（x）=x2-2x+m∈D，若存在，求出m的范围，若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案