


 OA交AB于N,连接CN,在△AOB中,
OA交AB于N,连接CN,在△AOB中,
 且OA=OB,
且OA=OB, 。在Rt△AON中,
。在Rt△AON中,
 ,
, 。
。


 .
. 。又AB=3AQ,
。又AB=3AQ, Q为AN的中点。在△CAN中,
Q为AN的中点。在△CAN中, 分别为AC,AN的中点,
分别为AC,AN的中点, .由OA
.由OA OC,OA
OC,OA ON知:OA
ON知:OA 平面CON。又NC
平面CON。又NC 平面CON,
平面CON, OA
OA CN.由PQ//CN,知OA
CN.由PQ//CN,知OA PQ.
PQ. 
 OA,OC
OA,OC OB知:OC
OB知:OC 平面OAB。
平面OAB。 平面OAB,
平面OAB, OC
OC ON.又由ON
ON.又由ON OA知:ON
OA知:ON 平面AOC.
平面AOC.  OP是NP在平面AOC内的射影。
OP是NP在平面AOC内的射影。 AC
AC OP。
OP。 NP.
NP.
 为二面角O-AC-B的平面角。
为二面角O-AC-B的平面角。 OP=
OP= 。
。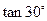 =
= ,
, 在Rt△PON中,PN=
在Rt△PON中,PN=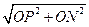 =
= ,
, cos
cos 。
。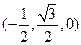 。
。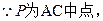
 。
。 。
。
 .
. .
. .故
.故 。
。 ,则由n
,则由n
 ,n
,n ,且
,且 =(1,0,-1)。
=(1,0,-1)。 故可取
故可取 。
。
 ,则
,则 。
。

科目:高中数学 来源:不详 题型:单选题
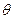 ,则sin
,则sin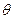
|
A. | B.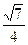 | C.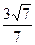 | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com