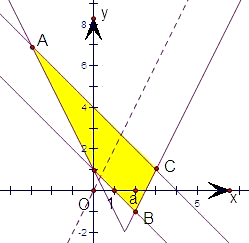
解:(1)作出满足约束条件
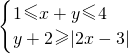
的可行域,如右图所示,
(2)由(1)可知,
①当直线z=y-ax的斜率a>2时,
直线z=y-ax平移到点A(-3,7)时,
目标函数z=y-ax取得最大值7+3a;
当直线z=y-ax平移到点C(3,1)时,
目标函数z=y-ax取得最小值-3a+1;
②当直线z=y-ax的斜率-1<a≤2时,
直线z=y-ax平移到点A(-3,7)时,
目标函数z=y-ax取得最大值7+3a;
当直线z=y-ax平移到点B(2,-1)时,
目标函数z=y-ax取得最小值-2a-1;
综上所述:最大值为7+3a,最小值为
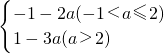
.
分析:(1)将点的坐标设出,据已知求出点的横坐标、纵坐标满足的约束条件,画出可行域,
(2)①观察(1)的可行域②z为目标函数纵截距③画直线y-ax=0,平移直线观察最值.
点评:本题考查不等式中的线性规划知识,画出平面区域与正确理解目标函数z=y-ax的几何意义是解答好本题的关键.

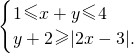
 解:(1)作出满足约束条件
解:(1)作出满足约束条件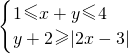 的可行域,如右图所示,
的可行域,如右图所示,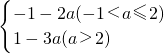 .
.

 字词句段篇系列答案
字词句段篇系列答案