
【题目】有1998名运动员号码为1~1998这1998个自然数,从中选出若干名运动员参加仪仗队,但要使剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.那么,选为仪仗队的运动员至少能有多少人?给出你的选取方案,并简述理由.
【答案】43
【解析】
可选出号码为![]() 这43名运动员去当仪仗队员作为选取方案,即可满足题目条件要求,理由如下:
这43名运动员去当仪仗队员作为选取方案,即可满足题目条件要求,理由如下:
因为选出这43名运动员作仪仗队员后,剩下运动员的号码(除1号外)的任何两个号码数的积将大于![]() .而1与任何一个号码数相乘不会等于第三个不同的数.所以,剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.
.而1与任何一个号码数相乘不会等于第三个不同的数.所以,剩下的运动员中没有一个人的号码数等于另外两人的号码数的乘积.
现在证明:43是选为仪仗队的运动员的最少人数.也就是证明:当选取42个运动员为仪仗队员后,余下的队员中至少有这样的三个号码数,其中两个号码数的乘积等于第三个号码数.为此,我们考察三数组.![]()
即 .
.
因为函数![]() 在区间
在区间![]() 上是递增的,所以,写出的数目是不相同的,并且都不超过
上是递增的,所以,写出的数目是不相同的,并且都不超过![]() .这样的三数组个数为43个.如果选出的运动员少于43个,至多为42个,上述43个三数组中,至少要有一组三个数都没被选,则这三个数作为被剩下的运动员的号码,其中一个数等于另外两数的乘积,就不满足题设条件要求了,所以,选为仪仗队的运动员至少要有43个.
.这样的三数组个数为43个.如果选出的运动员少于43个,至多为42个,上述43个三数组中,至少要有一组三个数都没被选,则这三个数作为被剩下的运动员的号码,其中一个数等于另外两数的乘积,就不满足题设条件要求了,所以,选为仪仗队的运动员至少要有43个.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知某手机品牌公司的年固定成本为40万元,每生产1万部手机还需要另投入16万元,设该公句一年内生产x万部并全部销售完,每1万部手机的销售收入为![]() 万元,且
万元,且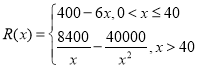 .
.
(1)写出年利润(万元)关于年产量![]() (万部)的函数解析式;
(万部)的函数解析式;
(2)当年产量多少万部时,公司在该款手机生产获得最大利润,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆O:![]() 与坐标轴分别交于A1,A2,B1,B2(如图).
与坐标轴分别交于A1,A2,B1,B2(如图).
(1)点Q是圆O上除A1,A2外的任意点(如图1),直线A1Q,A2Q与直线![]() 交于不同的两点M,N,求线段MN长的最小值;
交于不同的两点M,N,求线段MN长的最小值;
(2)点P是圆O上除A1,A2,B1,B2外的任意点(如图2),直线B2P交x轴于点F,直线A1B2交A2P于点E.设A2P的斜率为k,EF的斜率为m,求证:2m﹣k为定值.
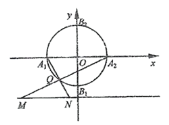
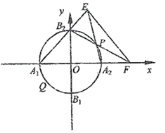
(图1) (图2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:①方程![]() 表示的图形是一个点;②命题“若
表示的图形是一个点;②命题“若![]() ,则
,则![]() 或
或![]() ”为真命题;③已知双曲线
”为真命题;③已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,过右焦点
,过右焦点![]() 被双曲线截得的弦长为4的直线有3条;④已知椭圆
被双曲线截得的弦长为4的直线有3条;④已知椭圆![]() :
:![]()
![]() 上有两点
上有两点![]() ,
,![]() ,若点
,若点![]() 是椭圆
是椭圆![]() 上任意一点,且
上任意一点,且![]() ,直线
,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,则
,则![]() 为定值
为定值![]() ;⑤已知命题“
;⑤已知命题“![]() ,
,![]() 满足
满足![]() ,
,![]() ”是真命题,则实数
”是真命题,则实数![]() .其中说法正确的序号是__________.
.其中说法正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在199319936688张卡片上,每张写上一个自然数,恰写了1,2,…,199319936688这199319936688个自然数.问能否把这些卡片分成三组,使得第二组卡片上写的数之总和比第一组卡片上写的数之总和大33,而第三组卡片上写的数之总和比第二组卡片上写的数之总和大102?
若能,请给出一种分组方法.若不能,请你说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出函数![]() 如下表,则f〔g(x)〕的值域为( )
如下表,则f〔g(x)〕的值域为( )
x | 1 | 2 | 3 | 4 |
g(x) | 1 | 1 | 3 | 3 |
x | 1 | 2 | 3 | 4 |
f(x) | 4 | 3 | 2 | 1 |
A. {4,2} B. {1,3} C. {1,2,3,4} D. 以上情况都有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某广场要划出一块矩形区域![]() ,在其中开辟三块完全相同的矩形绿化园圃,空白处均铺设
,在其中开辟三块完全相同的矩形绿化园圃,空白处均铺设![]() 宽的走道,如图.已知三块园圃的总面积为
宽的走道,如图.已知三块园圃的总面积为![]() ,设园圃小矩形的一边长为
,设园圃小矩形的一边长为![]() ,区域
,区域![]() 的面积为
的面积为![]() (单位:
(单位:![]() ).
).
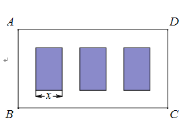
(1)求![]() 的最小值.
的最小值.
(2)若区域![]() 的面积不超过
的面积不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com