
现有5种不同颜色的染料,要对如图中的四个不同区域进行着色,要求有公共边的两块区域不能使用同一种颜色,则不同的着色方法的种数是 种.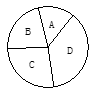
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
有甲、乙、丙、丁四名深圳大运会志愿者被随机地分到A,B,C三个不同的岗位服务,若A岗位需要两名志愿者,B,C岗位各需要一名志愿者。甲、乙两人同时不参加A岗位服务的概率是 ;甲不在A岗位,乙不在B岗位,丙不在C岗位,这样安排服务的概率是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com