
【题目】如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.

(1)求证: ![]() 面
面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】北京大学从参加逐梦计划自主招生考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组![]() ,
, ![]() ,…,
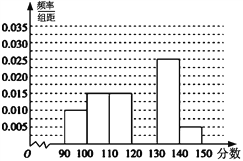
,…, ![]() 后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
(1)求分数在![]() 内的频率;
内的频率;
(2)估计本次考试成绩的中位数(结果四舍五入,保留整数);
(3)用分层抽样的方法在分数段为![]() 的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有
的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有![]() 人在分数段
人在分数段![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中, ![]() 的两个顶点
的两个顶点![]() 的坐标分别为
的坐标分别为![]() ,三个内角
,三个内角![]() 满足
满足![]() .
.
(1)若顶点![]() 的轨迹为
的轨迹为![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)若点![]() 为曲线
为曲线![]() 上的一点,过点
上的一点,过点![]() 作曲线
作曲线![]() 的切线交圆
的切线交圆![]() 于不同的两点
于不同的两点![]() (其中
(其中![]() 在
在![]() 的右侧),求四边形
的右侧),求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某礼品店要制作一批长方体包装盒,材料是边长为![]() 的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是
的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是![]() 的正方形,然后在余下两个角处各切去一个长、宽分别为
的正方形,然后在余下两个角处各切去一个长、宽分别为![]() 、
、![]() 的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.
的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.

(1)求包装盒的容积![]() 关于
关于![]() 的函数表达式,并求函数的定义域;
的函数表达式,并求函数的定义域;
(2)当![]() 为多少时,包装盒的容积最大?最大容积是多少?
为多少时,包装盒的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(![]() )证明数列
)证明数列![]() 是等比数列,求出数列
是等比数列,求出数列![]() 的通项公式.
的通项公式.
(![]() )设
)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(![]() )数列
)数列![]() 中是否存在三项,它们可以构成等比数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等比数列?若存在,求出一组符合条件的项;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,其图象上存在一点
,其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,方程
时,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com