
ЁОЬтФПЁПвбжЊФГЕиЧјФГжжРЅГцВњТбЪ§КЭЮТЖШгаЙи.ЯжЪеМЏСЫвЛжЛИУЦЗжжРЅГцЕФВњТбЪ§![]() ЃЈИіЃЉКЭЮТЖШ
ЃЈИіЃЉКЭЮТЖШ![]() ЃЈ
ЃЈ![]() ЃЉЕФ7зщЙлВтЪ§ОнЃЌЦфЩЂЕуЭМШчЫљЪОЃК
ЃЉЕФ7зщЙлВтЪ§ОнЃЌЦфЩЂЕуЭМШчЫљЪОЃК
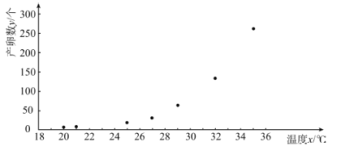
ИљОнЩЂЕуЭМЃЌНсКЯКЏЪ§жЊЪЖЃЌПЩвдЗЂЯжВњТбЪ§![]() КЭЮТЖШ
КЭЮТЖШ![]() ПЩгУЗНГЬ
ПЩгУЗНГЬ![]() РДФтКЯЃЌСю
РДФтКЯЃЌСю![]() ЃЌНсКЯбљБОЪ§ОнПЩжЊ
ЃЌНсКЯбљБОЪ§ОнПЩжЊ![]() гыЮТЖШ
гыЮТЖШ![]() ПЩгУЯпадЛиЙщЗНГЬРДФтКЯЃЎИљОнЪеМЏЕНЕФЪ§ОнЃЌМЦЫуЕУЕНШчЯТжЕЃК
ПЩгУЯпадЛиЙщЗНГЬРДФтКЯЃЎИљОнЪеМЏЕНЕФЪ§ОнЃЌМЦЫуЕУЕНШчЯТжЕЃК
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
Бэжа![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() КЭЮТЖШ
КЭЮТЖШ![]() ЕФЛиЙщЗНГЬЃЈЛиЙщЯЕЪ§НсЙћОЋШЗЕН
ЕФЛиЙщЗНГЬЃЈЛиЙщЯЕЪ§НсЙћОЋШЗЕН![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉЧѓВњТбЪ§![]() ЙигкЮТЖШ
ЙигкЮТЖШ![]() ЕФЛиЙщЗНГЬЃЛШєИУЕиЧјвЛЖЮЪБМфФкЕФЦјЮТдк
ЕФЛиЙщЗНГЬЃЛШєИУЕиЧјвЛЖЮЪБМфФкЕФЦјЮТдк![]() жЎМфЃЈАќРЈ
жЎМфЃЈАќРЈ![]() гы
гы![]() ЃЉЃЌЙРМЦИУЦЗжжвЛжЛРЅГцЕФВњТбЪ§ЕФЗЖЮЇ.ЃЈВЮПМЪ§ОнЃК
ЃЉЃЌЙРМЦИУЦЗжжвЛжЛРЅГцЕФВњТбЪ§ЕФЗЖЮЇ.ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎЃЉ
ЃЎЃЉ
ИНЃКЖдгквЛзщЪ§Он![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌЦфЛиЙщжБЯп
ЃЌЦфЛиЙщжБЯп![]() ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ
ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЗжБ№ЮЊ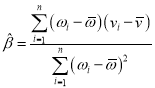 ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌ
ЃЌ![]() .
.
ЁОНтЮіЁП
(1)ИљОнЙЋЪНМЦЫуГі![]() КЭ
КЭ![]() ,ПЩЕУ
,ПЩЕУ![]() ;
;
(2)ИљОн![]() ПЩЕУ
ПЩЕУ![]() ,дйИљОнКЏЪ§
,дйИљОнКЏЪ§![]() ЮЊдіКЏЪ§ПЩЕУД№АИ.
ЮЊдіКЏЪ§ПЩЕУД№АИ.
ЃЈ1ЃЉвђЮЊ![]() гыЮТЖШ
гыЮТЖШ![]() ПЩвдгУЯпадЛиЙщЗНГЬРДФтКЯЃЌЩш
ПЩвдгУЯпадЛиЙщЗНГЬРДФтКЯЃЌЩш![]() ЃЎ
ЃЎ
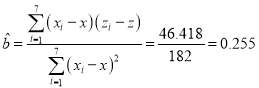 ЃЌ
ЃЌ
Ыљвд![]() ЃЌ
ЃЌ
ЙЪ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЮЊ
ЕФЯпадЛиЙщЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩЕУ![]() ЃЌ
ЃЌ
гкЪЧВњТбЪ§![]() ЙигкЮТЖШ
ЙигкЮТЖШ![]() ЕФЛиЙщЗНГЬЮЊ
ЕФЛиЙщЗНГЬЮЊ![]() ,
,
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
вђЮЊКЏЪ§![]() ЮЊдіКЏЪ§ЃЌ
ЮЊдіКЏЪ§ЃЌ
ЫљвдЃЌЦјЮТдк![]() жЎМфЪБЃЌвЛжЛИУЦЗжжРЅГцЕФВњТбЪ§ЕФЙРМЦЗЖЮЇЪЧ
жЎМфЪБЃЌвЛжЛИУЦЗжжРЅГцЕФВњТбЪ§ЕФЙРМЦЗЖЮЇЪЧ![]() ФкЕФе§ећЪ§ЃЎ
ФкЕФе§ећЪ§ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГОЯњЩЬДгФГбјжГГЁЙКНјФГЦЗжжКгаЗЃЌВЂЫцЛњГщШЁСЫ 100жЛНјааЭГМЦЃЌАДжиСПЗжРрЭГМЦЃЌЕУЕНЦЕТЪЗжВМжБЗНЭМШчЯТЃК
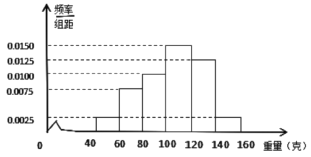
ЃЈ1ЃЉМЧЪТМў![]() ЮЊЁАДгетХњКгаЗжаШЮШЁвЛжЛЃЌжиСПВЛГЌЙ§120ПЫЁБЃЌЙРМЦ
ЮЊЁАДгетХњКгаЗжаШЮШЁвЛжЛЃЌжиСПВЛГЌЙ§120ПЫЁБЃЌЙРМЦ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЪдЙРМЦетХњКгаЗЕФЦНОљжиСПЃЛ
ЃЈ3ЃЉИУОЯњЩЬАДгаЙиЙцЖЈНЋИУЦЗжжКгаЗЗжШ§ИіЕШМЖЃЌВЂжЦЖЈГіЯњЪлЕЅМлШчЯТЃК
ЕШМЖ | ЬиМЖ | вЛМЖ | ЖўМЖ |
жиСП |
|
|
|
ЕЅМлЃЈдЊ/жЛЃЉ | 40 | 20 | 10 |
ЪдЙРЫуИУОЯњЩЬвдУПЧЇПЫжСЖрЛЈЖрЩйдЊЃЈШЁећЃЉЪеЙКетХњКгаЗЃЌВХФмЛёРћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ12ЗжЃЉШєЪ§Са{an}ЪЧЕФЕндіЕШВюЪ§СаЃЌЦфжаЕФa3=5ЃЌЧвa1ЃЌa2ЃЌa5ГЩЕШБШЪ§СаЃЌ
ЃЈ1ЃЉЧѓ{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉЩшbn= ![]() ЃЌЧѓЪ§Са{bn}ЕФЧАЯюЕФКЭTnЃЎ
ЃЌЧѓЪ§Са{bn}ЕФЧАЯюЕФКЭTnЃЎ
ЃЈ3ЃЉЪЧЗёДцдкздШЛЪ§mЃЌЪЙЕУ![]() ЃМTnЃМ
ЃМTnЃМ![]() ЖдвЛЧаnЁЪN*КуГЩСЂЃПШєДцдкЃЌЧѓГіmЕФжЕЃЛ
ЖдвЛЧаnЁЪN*КуГЩСЂЃПШєДцдкЃЌЧѓГіmЕФжЕЃЛ
ШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌШєЖдШЮвтЕФ
ЃЌШєЖдШЮвтЕФ![]() ЃЌГЄЮЊ
ЃЌГЄЮЊ![]() ЕФШ§ЬѕЯпЖЮОљПЩвдЙЙГЩШ§НЧаЮЃЌдђе§ЪЕЪ§
ЕФШ§ЬѕЯпЖЮОљПЩвдЙЙГЩШ§НЧаЮЃЌдђе§ЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЪЧ______.
ЕФШЁжЕЗЖЮЇЪЧ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшmЃЌnЮЊЦНУцІСЭтСНЬѕжБЯпЃЌЦфдкЦНУцІСФкЕФЩфгАЗжБ№ЪЧСНЬѕжБЯпm1КЭn1ЃЌИјГіЯТСа4ИіУќЬтЃКЂйm1ЁЮn1mЁЮnЃЛЂкmЁЮnm1гыn1ЦНааЛђжиКЯЃЛЂлm1ЁЭn1mЁЭnЃЛЂмmЁЭnm1ЁЭn1ЃЎЦфжаЫљгаМйУќЬтЕФађКХЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
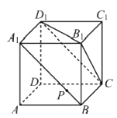
ЁОЬтФПЁПШчЭМЃЌдке§ЗНЬх![]() жаЃЌЕу
жаЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯвЦЖЏЃЌгаЯТСаХаЖЯЃКЂйЦНУц
ЩЯвЦЖЏЃЌгаЯТСаХаЖЯЃКЂйЦНУц![]() ЦНУц
ЦНУц![]() ЃЛЂкЦНУц
ЃЛЂкЦНУц![]() ЦНУц
ЦНУц![]() ЃЛЂлШ§РтзЖ
ЃЛЂлШ§РтзЖ![]() ЕФЬхЛ§ВЛБфЃЛЂм
ЕФЬхЛ§ВЛБфЃЛЂм![]() ЦНУц
ЦНУц![]() ЃЎЦфжаЃЌе§ШЗЕФЪЧ______ЃЎЃЈАбЫљгае§ШЗЕФХаЖЯЕФађКХЖМЬюЩЯЃЉ
ЃЎЦфжаЃЌе§ШЗЕФЪЧ______ЃЎЃЈАбЫљгае§ШЗЕФХаЖЯЕФађКХЖМЬюЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§fЃЈxЃЉЃН6cos2![]() sinІиxЉ3ЃЈІиЃО0ЃЉдквЛИіжмЦкФкЕФЭМЯѓШчЭМЫљЪОЃЌAЮЊЭМЯѓЕФзюИпЕуЃЌBЃЌCЮЊЭМЯѓгыxжсЕФНЛЕуЃЌЧвЁїABCЮЊе§Ш§НЧаЮ
sinІиxЉ3ЃЈІиЃО0ЃЉдквЛИіжмЦкФкЕФЭМЯѓШчЭМЫљЪОЃЌAЮЊЭМЯѓЕФзюИпЕуЃЌBЃЌCЮЊЭМЯѓгыxжсЕФНЛЕуЃЌЧвЁїABCЮЊе§Ш§НЧаЮ
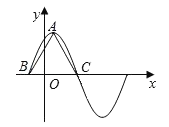
ЃЈ1ЃЉЧѓІиЕФжЕМАКЏЪ§fЃЈxЃЉЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєfЃЈx0ЃЉ![]() ЃЌЧвx0ЁЪЃЈ
ЃЌЧвx0ЁЪЃЈ![]() ЃЉЃЌЧѓfЃЈx0+1ЃЉЕФжЕ
ЃЉЃЌЧѓfЃЈx0+1ЃЉЕФжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§![]() ЃЈ
ЃЈ![]() ЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЉдк
ЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЉдк![]() ЕФЖЈвхгђЩЯЕЅЕїЕндіЃЌдђГЦКЏЪ§
ЕФЖЈвхгђЩЯЕЅЕїЕндіЃЌдђГЦКЏЪ§![]() Опга
Опга![]() аджЪ.ЯТСаКЏЪ§жаЫљгаОпга
аджЪ.ЯТСаКЏЪ§жаЫљгаОпга![]() аджЪЕФКЏЪ§ЕФађКХЮЊЃЈ ЃЉ
аджЪЕФКЏЪ§ЕФађКХЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛжжжРїЛзгзпЬјЦхЕФгЮЯЗЃКЦхХЬЩЯБъгаЕк0еОЁЂЕк1еОЁЂЕк2еОЁЂЁЁЂЕк100еОЃЌЙВ101еОЃЌЩшЦхзгЬјЕНЕкnеОЕФИХТЪЮЊ![]() ЃЌвЛУЖЦхзгПЊЪМдкЕк0еОЃЌЦхЪжУПжРвЛДЮїЛзгЃЌЦхзгЯђЧАЬјЖЏвЛДЮЃЎШєжРГіЦцЪ§ЕуЃЌЦхзгЯђЧАЬјвЛеОЃЛШєжРГіХМЪ§ЕуЃЌЦхзгЯђЧАЬјСНеОЃЌжБЕНЦхзгЬјЕНЕк99еО(ЛёЪЄ)ЛђЕк100еО(ЪЇАм)ЪБЃЌгЮЯЗНсЪј(їЛзгЪЧгУвЛжжОљдШВФСЯзіГЩЕФСЂЗНЬхаЮзДЕФгЮЯЗЭцОпЃЌЫќЕФСљИіУцЗжБ№БъгаЕуЪ§1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6)ЃЎ
ЃЌвЛУЖЦхзгПЊЪМдкЕк0еОЃЌЦхЪжУПжРвЛДЮїЛзгЃЌЦхзгЯђЧАЬјЖЏвЛДЮЃЎШєжРГіЦцЪ§ЕуЃЌЦхзгЯђЧАЬјвЛеОЃЛШєжРГіХМЪ§ЕуЃЌЦхзгЯђЧАЬјСНеОЃЌжБЕНЦхзгЬјЕНЕк99еО(ЛёЪЄ)ЛђЕк100еО(ЪЇАм)ЪБЃЌгЮЯЗНсЪј(їЛзгЪЧгУвЛжжОљдШВФСЯзіГЩЕФСЂЗНЬхаЮзДЕФгЮЯЗЭцОпЃЌЫќЕФСљИіУцЗжБ№БъгаЕуЪ§1ЃЌ2ЃЌ3ЃЌ4ЃЌ5ЃЌ6)ЃЎ
(1)Чѓ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌВЂИљОнЦхзгЬјЕНЕкnеОЕФЧщПіЃЌЪдгУ
ЃЌВЂИљОнЦхзгЬјЕНЕкnеОЕФЧщПіЃЌЪдгУ![]() КЭ
КЭ![]() БэЪО
БэЪО![]() ЃЛ
ЃЛ
(2)ЧѓжЄЃК![]() ЮЊЕШБШЪ§СаЃЛ
ЮЊЕШБШЪ§СаЃЛ
(3)ЧѓЭцИУгЮЯЗЛёЪЄЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com