
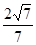
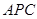 内找一条与
内找一条与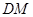 平行的直线,根据题意可知,
平行的直线,根据题意可知, 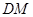 是
是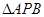 的中位线,有
的中位线,有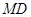 ∥
∥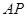 ,则证明.
,则证明.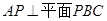 ,从而得到
,从而得到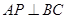 ,进而有
,进而有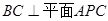 ,最终可证
,最终可证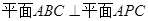 .
.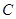 作
作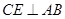 ,垂足为
,垂足为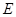 ,连接
,连接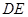 ,猜想
,猜想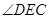 为二面角
为二面角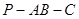 的平面角,根据二面角的平面角定义,只需证明
的平面角,根据二面角的平面角定义,只需证明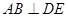 ,显然根据已知以及(1)中的结论,可证
,显然根据已知以及(1)中的结论,可证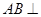 平面
平面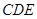 ,则可证明猜想.将
,则可证明猜想.将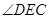 放入
放入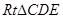 中,即可求其正弦值.
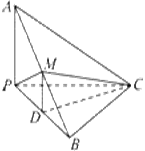
中,即可求其正弦值.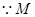 为
为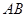 中点,
中点, 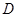 为
为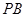 中点,
中点, 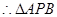 中,有
中,有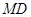 ∥
∥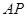 ,
,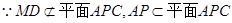 ,
, 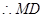 ∥平面
∥平面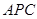
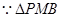 为正三角形,且
为正三角形,且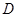 为
为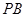 中点,
中点, 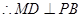
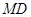 ∥
∥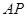 .
.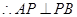
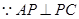 ,
, 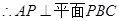
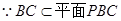
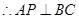
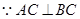
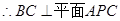
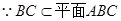
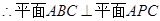
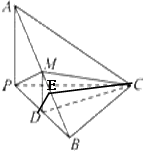
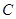 作
作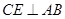 ,垂足为
,垂足为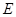 ,连接
,连接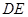 ,
, 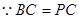 ,
,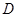 为
为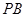 中点,
中点,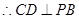 ,又由(2)知
,又由(2)知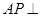 平面
平面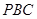 ,
,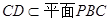
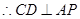 ,
,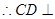 平面
平面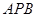 ,
,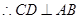
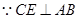
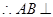 平面
平面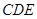 ,
,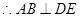
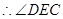 为二面角
为二面角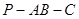 的平面角
的平面角 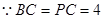 ,
,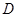 为
为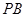 中点,,又由(2)
中点,,又由(2)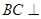 平面
平面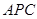 ,∴
,∴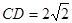 ,
,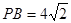 ,
,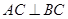 ,
,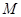 为
为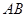 中点,
中点,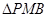 为正三角形,
为正三角形,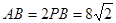 ,
,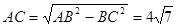 ,
,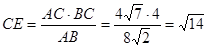
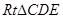 ,
,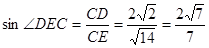
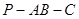 的正弦值为
的正弦值为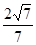 .
. 

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
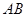 是圆
是圆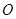 的直径,点
的直径,点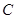 是圆
是圆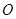 上异于
上异于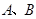 的点,直线
的点,直线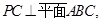
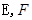 分别为
分别为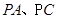 的中点。
的中点。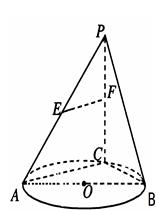
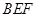 与平面
与平面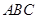 的交线为
的交线为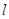 ,试判断
,试判断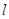 与平面
与平面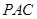 的位置关系,并加以说明;
的位置关系,并加以说明;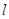 与圆
与圆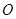 的另一个交点为
的另一个交点为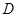 ,且点
,且点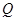 满足
满足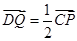 ,记直线
,记直线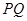
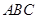 所成的角为
所成的角为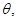 异面直线
异面直线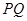 与
与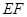 所成的锐角为
所成的锐角为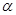 ,二面角
,二面角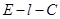 的大小为
的大小为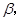
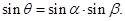
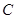 为弧
为弧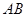 的中点时,
的中点时,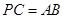 ,求直线
,求直线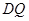 与平面
与平面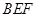 所成的角的正弦值。
所成的角的正弦值。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.若b?α,c∥α,则c∥b |
| B.若b?α,b∥c,则c∥α |
| C.若c?α,α⊥β,则c⊥β |
| D.若c?α,c⊥β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.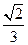 | B.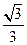 | C.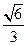 | D.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com