
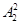 =2种排法;第二类:工程丙、丁占据4,5位置,共有(
=2种排法;第二类:工程丙、丁占据4,5位置,共有(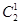 +1)·
+1)·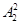 =6种排法;第三类:工程丙、丁占据5,6位置,共有(
=6种排法;第三类:工程丙、丁占据5,6位置,共有(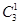 +
+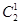 +1)·
+1)·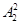 =12种排法.
=12种排法.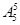 种排法.在所有的这些排法中,考虑甲、乙、丙相对顺序共有
种排法.在所有的这些排法中,考虑甲、乙、丙相对顺序共有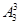 种,故满足条件的排法种数为
种,故满足条件的排法种数为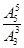 =20种.
=20种.

科目:高中数学 来源:不详 题型:解答题
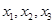 ,随机变量
,随机变量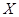 表示
表示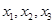 的最大数,求
的最大数,求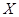 的概率分布和数学期望
的概率分布和数学期望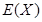 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.6个 | B.9个 | C.18个 | D.36个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.96 | B.114 | C.128 | D.136 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com