
【题目】如图所示,在三棱柱![]() 中,
中,![]() 平面
平面![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 是线段
是线段![]() 上的中点.
上的中点.
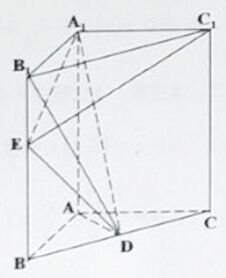
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,且直线
,且直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,试指出点
,试指出点![]() 在线段
在线段![]() 上的位置,并求三棱锥
上的位置,并求三棱锥![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】为了比较注射![]() ,
,![]() 两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .下表1和表2分别是注射药物
.下表1和表2分别是注射药物![]() 和药物
和药物![]() 后的实验结果.(疱疹面积单位:
后的实验结果.(疱疹面积单位:![]() )
)
表1:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
疱疹面积 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
疱疹面积 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
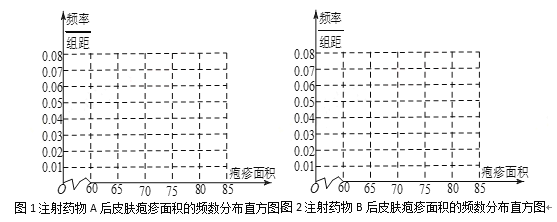
(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(2)完成下面![]() 列联表,并回答能否有99.9%的把握认为“注射药物
列联表,并回答能否有99.9%的把握认为“注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 后的疱疹面积有差异”.
后的疱疹面积有差异”.
疱疹面积小于 | 疱疹面积不小于 | 合计 | |
注射药物 | |||
注射药物 | |||
合计 |
附: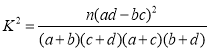
| 0.100 | 0.050 | 0.025 | 0.01 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx﹣2mx+x2(m>0).
(1)讨论函数f(x)的单调性;
(2)当![]() 时,若函数f(x)的导函数f′(x)的图象与x轴交于A,B两点,其横坐标分别为x1,x2(x1<x2),线段AB的中点的横坐标为x0,且x1,x2恰为函数h(x)=lnx﹣cx2﹣bx的零点.求证(x1﹣x2)h'(x0)≥
时,若函数f(x)的导函数f′(x)的图象与x轴交于A,B两点,其横坐标分别为x1,x2(x1<x2),线段AB的中点的横坐标为x0,且x1,x2恰为函数h(x)=lnx﹣cx2﹣bx的零点.求证(x1﹣x2)h'(x0)≥![]() +ln2.
+ln2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
(1)命题![]() ,使得
,使得![]() ,则
,则![]() ,都有
,都有![]() ;
;
(2)已知函数f(x)=|log2x|,若a≠b,且f(a)=f(b),则ab=1;
(3)若平面α内存在不共线的三点到平面β的距离相等,则平面α平行于平面β;
(4)已知定义在![]() 上的函数
上的函数![]() 满足条件
满足条件![]() ,且函数
,且函数![]() 为奇函数,则函数
为奇函数,则函数![]() 的图象关于点
的图象关于点![]() 对称.
对称.
其中真命题的序号为______________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O是平面直角坐标系的原点,双曲线![]() .
.
(1)过双曲线![]() 的右焦点
的右焦点![]() 作x轴的垂线,交
作x轴的垂线,交![]() 于A、B两点,求线段AB的长;
于A、B两点,求线段AB的长;
(2)设M为![]() 的右顶点,P为
的右顶点,P为![]() 右支上任意一点,已知点T的坐标为
右支上任意一点,已知点T的坐标为![]() ,当
,当![]() 的最小值为
的最小值为![]() 时,求t的取值范围;
时,求t的取值范围;
(3)设直线![]() 与
与![]() 的右支交于A,B两点,若双曲线右支上存在点C使得
的右支交于A,B两点,若双曲线右支上存在点C使得![]() ,求实数m的值和点C的坐标.
,求实数m的值和点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() .
.
(1)若直线![]() 不经过第四象限,求
不经过第四象限,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,
,![]() 为坐标原点,设
为坐标原点,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com