
| A. | 2π | B. | $\frac{5}{2}π$ | C. | eπ | D. | 3π |
分析 根据已知中关于“莫言函数”,“莫言点”,“莫言圆”的定义,利用a=1,b=1,我们易求出“莫言点”坐标,并设出“莫言圆”的方程,根据两点的距离公式求出圆心到“莫言函数”图象上点的最小距离,即可得到结论.
解答 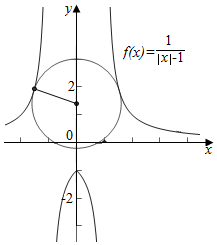 解:当a=1且b=1时,函数“莫言函数”为y=$\frac{1}{|x|-1}$
解:当a=1且b=1时,函数“莫言函数”为y=$\frac{1}{|x|-1}$
图象与y轴交于(0,-1)点,则“莫言点”坐标为(0,1).
令“莫言圆”的标准方程为x2+(y-1)2=r2,
令“莫言圆”与函数y=$\frac{1}{|x|-1}$图象的左右两支相切,
则可得切点坐标为($\frac{1+\sqrt{5}}{2}$,$\frac{1+\sqrt{5}}{2}$)和(-$\frac{1+\sqrt{5}}{2}$,$\frac{1+\sqrt{5}}{2}$),
此时“莫言圆”的半径r=$\sqrt{3}$;
令“莫言圆”与函数$\frac{1}{|x|-1}$图象的下支相切,
此时切点坐标为(0,-1).
此时“莫言圆”的半径r=2;
故所有的“莫言圆”中,面积的最小值为3π.
故选:D.
点评 本题给出“莫言函数”、“莫言点”、“莫言圆”的定义,求圆的最小面积.着重考查了函数的图象、圆的方程、两点的距离公式与圆面积求法等知识,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥S-ABCD是底面ABCD为等腰梯形,CD∥AB,AC⊥BD,垂足为O,侧面SAD⊥底面ABCD,且∠ADS=$\frac{π}{2}$,AB=8,AD=$\sqrt{34}$,SD=$\sqrt{30}$,M为BS的中点.
如图所示,四棱锥S-ABCD是底面ABCD为等腰梯形,CD∥AB,AC⊥BD,垂足为O,侧面SAD⊥底面ABCD,且∠ADS=$\frac{π}{2}$,AB=8,AD=$\sqrt{34}$,SD=$\sqrt{30}$,M为BS的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理y(分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com