
【题目】已知自变量为![]() 的函数
的函数![]() 的极大值点为
的极大值点为![]() ,
,![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() ,证明:
,证明:![]() 有且仅有2个零点;
有且仅有2个零点;
(2)若![]() ,
,![]() ,
,![]() ,…,
,…,![]() 为任意正实数,证明:
为任意正实数,证明:![]() .
.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)当![]() 时,
时,![]() ,求导得
,求导得![]() ,令
,令![]() ,再次求导
,再次求导![]() ,可判断
,可判断![]() 在
在![]() 单调递减,又
单调递减,又![]() ,故
,故![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减;求得
上单调递减;求得![]() ,再判断
,再判断![]() ,
,![]() ,结合零点存在定理判断,
,结合零点存在定理判断,![]() 有且仅有2个零点;
有且仅有2个零点;
(2)对![]() 求导可得
求导可得![]() ,又
,又![]() ,故可判断
,故可判断![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减;故
上单调递减;故![]() 且
且![]() ,所求问题转化为
,所求问题转化为![]() ,
,
记![]() 为
为![]() ,观察知
,观察知![]() 为等差乘以等比数列的形式,结合错位相减法化简即可求证;
为等差乘以等比数列的形式,结合错位相减法化简即可求证;
解:(1)由题知:![]() ,
,
∴![]() ,令
,令![]() ,
,![]() ,
,
∴![]() 在
在![]() 单调递减,又∵
单调递减,又∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减;所以
上单调递减;所以![]() ;
;
又因为![]() ,
,![]() ,
,
所以![]() 在
在![]() ,
,![]() 上各恰有零点,即
上各恰有零点,即![]() 有且仅有2个零点.
有且仅有2个零点.
(2)由题知![]() ,
,
因此![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,
故![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减;
上单调递减;
因此![]() 且
且![]() ,
,
∵![]() ,所以
,所以![]() ,
,
记![]() 为
为![]() ,所以
,所以![]() ,
,
![]() ,
,
所以![]() ,
,
所以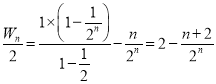 ,
,
所以![]() ,
,
因此![]() ,即
,即![]() .
.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 为正三角形,四边形ABCD为直角梯形,
为正三角形,四边形ABCD为直角梯形,![]() //
//![]() ,平面
,平面![]() 平面ABCD,点E,F分别为AD,CP的中点,
平面ABCD,点E,F分别为AD,CP的中点,![]() .
.
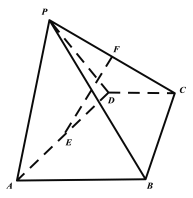
(1)证明:直线![]() //平面PAB;
//平面PAB;
(2)求直线EF与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求直线
,求直线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,点
两点,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网上购物是用户使用手机或电脑对所消费的商品或服务进行网络账务支付的一种服务方式,外卖、购物、买票等等我们生活的各个方面都可以通过网上来实现,某网络公司通过随机问卷调查,得到不同年龄段的网民在网上购物的情况.并从参与调查者中随机抽取了![]() 人.经统计得到如下表格:
人.经统计得到如下表格:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
在网上购物的人数 |
|
|
|
|
|
|
若把年龄大于或等于![]() 而小于
而小于![]() 岁的视为青少年,把年龄大于或等于
岁的视为青少年,把年龄大于或等于![]() 而小于
而小于![]() 岁的视为中年.把年龄大于或等于
岁的视为中年.把年龄大于或等于![]() 岁的视为老年,将频率视为概率.求:
岁的视为老年,将频率视为概率.求:
(1)在青少年,中年,老年中,哪个群休网上购物的概率最大?
(2)现从某市青少年网民(人数众多)中随机抽取![]() 人,设其中网上购物的人数为
人,设其中网上购物的人数为![]() .求随机变量
.求随机变量![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年初,某高级中学教务处为了解该高级中学学生的作文水平,从该高级中学学生某次考试成绩中按文科、理科用分层抽样方法抽取![]() 人的成绩作为样本,得到成绩频率分布直方图如图所示,
人的成绩作为样本,得到成绩频率分布直方图如图所示,![]() ,参考的文科生与理科生人数之比为
,参考的文科生与理科生人数之比为![]() ,成绩(单位:分)分布在
,成绩(单位:分)分布在![]() 的范围内且将成绩(单位:分)分为
的范围内且将成绩(单位:分)分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六个部分,规定成绩分数在
六个部分,规定成绩分数在![]() 分以及
分以及![]() 分以上的作文被评为“优秀作文”,成绩分数在50分以下的作文被评为“非优秀作文”.
分以上的作文被评为“优秀作文”,成绩分数在50分以下的作文被评为“非优秀作文”.

(1)求实数![]() 的值;
的值;
(2)(i)完成下面![]() 列联表;
列联表;
文科生/人 | 理科生/人 | 合计 | |
优秀作文 | 6 | ______ | ______ |
非优秀作文 | ______ | ______ | ______ |
合计 | ______ | ______ | 400 |
(ii)以样本数据研究学生的作文水平,能否在犯错误的概率不超过![]() 的情况下认为获得“优秀作文”与学生的“文理科“有关?
的情况下认为获得“优秀作文”与学生的“文理科“有关?
注: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90后从事互联网行业岗位分布条形图,则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.


A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的![]()
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学知识比赛中共有6个不同的题目,每位同学从中随机抽取3个题目进行作答,已知这6个题目中,甲只能正确作答其中的4个,而乙正确作答每个题目的概率均为![]() ,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
(1)求甲、乙两位同学总共正确作答3个题目的概率;
(2)若甲、乙两位同学答对题目个数分别是![]() ,
,![]() ,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和
,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com