
【题目】已知四棱锥S﹣ABCD的底面为矩形,SA⊥底面ABCD,点E在线段BC上,以AD为直径的圆过点 E.若SA=![]() AB=3,则△SED面积的最小值为_____.
AB=3,则△SED面积的最小值为_____.
【答案】![]()
【解析】
设BE=x,EC=y,则BC=AD=x+y,推导出SA⊥ED,ED⊥平面SAE,ED⊥SE,AE=![]() ,ED=
,ED=![]() ,推导出
,推导出![]() ,SE=
,SE=![]() ,ED=
,ED=![]() ,从而S△SED=
,从而S△SED=![]() ×SE×ED=
×SE×ED=![]() 由此能求出SED面积的最小值.
由此能求出SED面积的最小值.
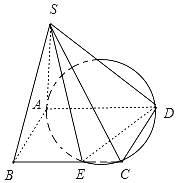
解:设BE=x,EC=y,则BC=AD=x+y,
∵SA⊥平面ABCD,ED平面ABCD,
∴SA⊥ED,
∵AE⊥ED,SA∩AE=A,∴ED⊥平面SAE,
∴ED⊥SE,
由题意得AE=![]() ,ED=
,ED=![]() ,
,
在Rt△AED中,AE2+ED2=AD2,
∴x2+3+y2+3=(x+y)2,化简,得xy=3,
在Rt△SED中,SE=![]() ,ED=
,ED=![]() =
=![]() ,
,
∴S△SED=![]() =
=![]() ,
,
∵3x2+![]() ≥2
≥2![]() =36,
=36,
当且仅当x=![]() ,
,
![]() 时,等号成立,
时,等号成立,
∴![]() =
=![]() ,
,
∴△SED面积的最小值为![]() ,
,
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C、D的动点,将△ADE沿AE翻折成△SAE,在翻折过程中,下列三个说法中正确的个数是( )
①存在点E和某一翻折位置使得AE∥平面SBC;
②存在点E和某一翻折位置使得SA⊥平面SBC;
③二面角S﹣AB﹣E的平面角总是小于2∠SAE.
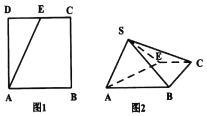
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谢尔宾斯基三角形(Sierpinski triangle)是一种分形几何图形,由波兰数学家谢尔宾斯基在1915年提出,它是一个自相似的例子,其构造方法是:
(1)取一个实心的等边三角形(图1);
(2)沿三边中点的连线,将它分成四个小三角形;
(3)挖去中间的那一个小三角形(图2);
(4)对其余三个小三角形重复(1)(2)(3)(4)(图3).
制作出来的图形如图4,….
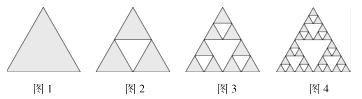
若图1(阴影部分)的面积为1,则图4(阴影部分)的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率是
的离心率是![]() ,斜率不为0的直线
,斜率不为0的直线![]() :
:![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() .
.
(1)若![]() 、
、![]() 分别是
分别是![]() 的左、右焦点,当
的左、右焦点,当![]() 经过
经过![]() 且
且![]() 时,求
时,求![]() 的值;
的值;
(2)试探究,是否存在点![]() ,使得
,使得![]() ?若存在,请写出满足条件的
?若存在,请写出满足条件的![]() 、
、![]() 的关系式;若不存在,说明理由.
的关系式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为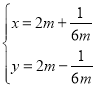 (m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+
(m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+![]() )=1.
)=1.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)已知点M (2,0),若直线l与曲线C相交于P、Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】至![]() 年底,我国发明专利申请量已经连续
年底,我国发明专利申请量已经连续![]() 年位居世界首位,下表是我国
年位居世界首位,下表是我国![]() 年至
年至![]() 年发明专利申请量以及相关数据.
年发明专利申请量以及相关数据.
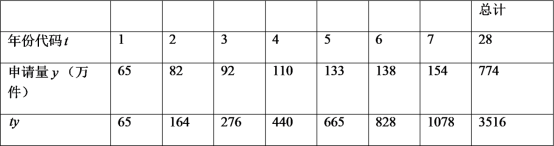
注:年份代码![]() ~
~![]() 分别表示
分别表示![]() ~
~![]() .
.
(1)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到
的回归直线方程(精确到![]() ),并预测我国发明专利申请量突破
),并预测我国发明专利申请量突破![]() 万件的年份.
万件的年份.
参考公式:回归直线的斜率和截距的最小二乘法估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】峰谷电是目前在城市居民当中开展的一种电价类别.它是将一天24小时划分成两个时间段,把8:00—22:00共14小时称为峰段,执行峰电价,即电价上调;22:00—次日8:00共10个小时称为谷段,执行谷电价,即电价下调.为了进一步了解民众对峰谷电价的使用情况,从某市一小区随机抽取了50 户住户进行夏季用电情况调查,各户月平均用电量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:度)分组的频率分布直方图如下图:
(单位:度)分组的频率分布直方图如下图:

若将小区月平均用电量不低于700度的住户称为“大用户”,月平均用电量低于700度的住户称为“一般用户”.其中,使用峰谷电价的户数如下表:
月平均用电量(度) |
|
|
|
|
|
|
使用峰谷电价的户数 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估计所抽取的 50户的月均用电量的众数和平均数(同一组中的数据用该组区间的中点值作代表);
(2)(![]() )将“一般用户”和“大用户”的户数填入下面
)将“一般用户”和“大用户”的户数填入下面![]() 的列联表:
的列联表:
一般用户 | 大用户 | |
使用峰谷电价的用户 | ||
不使用峰谷电价的用户 |
(![]() )根据(
)根据(![]() )中的列联表,能否有
)中的列联表,能否有![]() 的把握认为 “用电量的高低”与“使用峰谷电价”有关?
的把握认为 “用电量的高低”与“使用峰谷电价”有关?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com