
【题目】在一个半径为2的钢球内放置一个用来盛特殊液体的正四棱柱容器,要使该容器所盛液体尽可能多,则该容器的高应为_____.
科目:高中数学 来源: 题型:
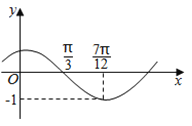
【题目】数![]() (其中
(其中![]() )的图象如图所示,为了得到
)的图象如图所示,为了得到![]() 的图象,则只要将
的图象,则只要将![]() 的图象上所有的点( )
的图象上所有的点( )
A.向左平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
B.向左平移![]() 个单位长度,纵坐标伸长到原来的3倍横坐标不变
个单位长度,纵坐标伸长到原来的3倍横坐标不变
C.向右平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
D.向右平移![]() 个单位长度,纵坐标伸长到原来的3倍,横坐标不变
个单位长度,纵坐标伸长到原来的3倍,横坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂加工的零件按箱出厂,每箱有10个零件,在出厂之前需要对每箱的零件作检验,人工检验方法如下:先从每箱的零件中随机抽取4个零件,若抽取的零件都是正品或都是次品,则停止检验;若抽取的零件至少有1个至多有3个次品,则对剩下的6个零件逐一检验.已知每个零件检验合格的概率为0.8,每个零件是否检验合格相互独立,且每个零件的人工检验费为2元.
(1)设1箱零件人工检验总费用为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工检验方法外还有机器检验方法,机器检验需要对每箱的每个零件作检验,每个零件的检验费为1.6元.现有1000箱零件需要检验,以检验总费用的数学期望为依据,在人工检验与机器检验中,应该选择哪一个?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,是否存在整数
时,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在极坐标系中,曲线C1是以C1(4,0)为圆心的半圆,曲线C2是以![]() 为圆心的圆,曲线C1、C2都过极点O.
为圆心的圆,曲线C1、C2都过极点O.

(1)分别写出半圆C1,C2的极坐标方程;
(2)直线l:![]() 与曲线C1,C2分别交于M、N两点(异于极点O),P为C2上的动点,求△PMN面积的最大值.
与曲线C1,C2分别交于M、N两点(异于极点O),P为C2上的动点,求△PMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中.已知:数列
这三个条件中任选一个,补充在下面问题中.已知:数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() , .求:对大于1的自然数
, .求:对大于1的自然数![]() ,是否存在大于2的自然数
,是否存在大于2的自然数![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列.若存在,求
成等比数列.若存在,求![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 上任意一点到两个焦点的距离和为4,且离心率为
上任意一点到两个焦点的距离和为4,且离心率为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)过![]() 作互相垂直的两条直线分别与椭圆
作互相垂直的两条直线分别与椭圆![]() 交于
交于![]() ,
,![]() 和
和![]() ,
,![]() ,设
,设![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,试探究直线
,试探究直线![]() 是否过定点?若是,求出该定点;若不是,说明理由.
是否过定点?若是,求出该定点;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的![]() ,
,![]() ,
,![]() 三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
三个不同车间生产同一产品的数量(单位:件)如下表所示.质检人员用分层抽样的方法从这些产品中共抽取6件样品进行检测:
车间 |
|
|
|
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自![]() ,
,![]() ,
,![]() 各车间产品的数量;
各车间产品的数量;
(2)若在这6件样品中随机抽取2件进行进一步检测,求这2件产品来自相同车间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com