
【题目】已知 ,则方程
,则方程![]() 恰有2个不同的实根,实数
恰有2个不同的实根,实数![]() 取值范围__________________.
取值范围__________________.
【答案】![]()
【解析】
将问题转化为当直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点时,求实数
个交点时,求实数![]() 的取值范围,并作出函数
的取值范围,并作出函数![]() 的图象,考查当直线
的图象,考查当直线![]() 与曲线
与曲线![]() 相切以及直线
相切以及直线![]() 与直线
与直线![]() 平行这两种临界位置情况,结合斜率的变化得出实数
平行这两种临界位置情况,结合斜率的变化得出实数![]() 的取值范围。
的取值范围。
问题等价于当直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点时,求实数
个交点时,求实数![]() 的取值范围。
的取值范围。
作出函数![]() 的图象如下图所示:
的图象如下图所示:
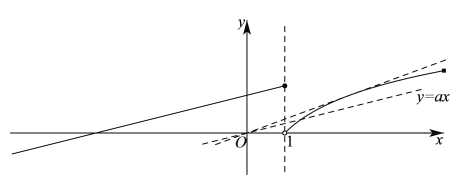
先考虑直线![]() 与曲线
与曲线![]() 相切时,
相切时,![]() 的取值,
的取值,
设切点为![]() ,对函数
,对函数![]() 求导得
求导得![]() ,切线方程为
,切线方程为![]() ,
,
即![]() ,则有
,则有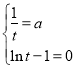 ,解得
,解得![]() .
.
由图象可知,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象没有公共点,在
上的图象没有公共点,在![]() 有一个公共点,不合乎题意;
有一个公共点,不合乎题意;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象没有公共点,在
上的图象没有公共点,在![]() 有两个公共点,合乎题意;
有两个公共点,合乎题意;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象只有一个公共点,在
上的图象只有一个公共点,在![]() 有两个公共点,不合乎题意;
有两个公共点,不合乎题意;
当![]() 时,直线
时,直线![]() 与函数
与函数![]() 在
在![]() 上的图象只有一个公共点,在
上的图象只有一个公共点,在![]() 没有公共点,不合乎题意.
没有公共点,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ,故答案为:
,故答案为:![]() .
.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】某地区为了了解本年度数学竞赛成绩情况,从中随机抽取了![]() 个学生的分数作为样本进行统计,按照
个学生的分数作为样本进行统计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图所示,已知得分在
的分组作出频率分布直方图如图所示,已知得分在![]() 的频数为20,且分数在70分及以上的频数为27.
的频数为20,且分数在70分及以上的频数为27.
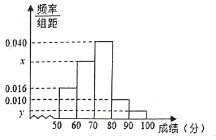
(1)求样本容量![]() 以及
以及![]() ,
,![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(1)证明|EA|+|EB|为定值,并写出点E的轨迹方程;
(2)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80 m.经测量,点A位于点O正北方向60 m处,点C位于点O正东方向170 m处(OC为河岸),tan∠BCO=![]() .
.
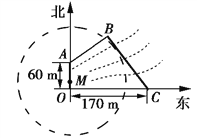
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区的各景点从2009年取消门票实行免费开放后,旅游的人数不断地增加,不仅带动了该市淡季的旅游,而且优化了旅游产业的结构,促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变.下表是从2009年至2018年,该景点的旅游人数![]() (万人)与年份
(万人)与年份![]() 的数据:
的数据:
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
旅游人数 | 300 | 283 | 321 | 345 | 372 | 435 | 486 | 527 | 622 | 800 |
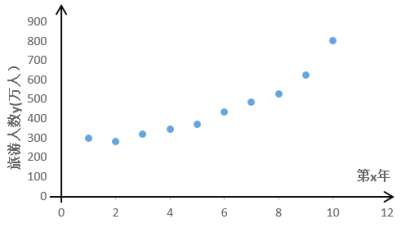
该景点为了预测2021年的旅游人数,建立了![]() 与
与![]() 的两个回归模型:
的两个回归模型:
模型①:由最小二乘法公式求得![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ;
;
模型②:由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近.
的附近.
(1)根据表中数据,求模型②的回归方程![]() .(
.(![]() 精确到个位,
精确到个位,![]() 精确到0.01).
精确到0.01).
(2)根据下列表中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
回归方程 | ① | ② |
| 30407 | 14607 |
参考公式、参考数据及说明:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为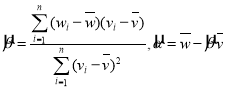 .②刻画回归效果的相关指数
.②刻画回归效果的相关指数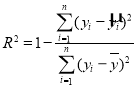 ;③参考数据:
;③参考数据:![]() ,
,![]() .
.
|
|
|
|
|
|
5.5 | 449 | 6.05 | 83 | 4195 | 9.00 |
表中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .例如:10点04分,记作时刻64.
.例如:10点04分,记作时刻64.

(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将宽和长都分别为x,![]() 的两个矩形部分重叠放在一起后形成的正十字形面积为
的两个矩形部分重叠放在一起后形成的正十字形面积为![]() 注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形
注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形![]() ,
,
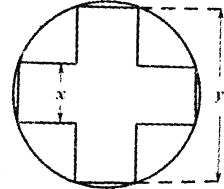
![]() 求y关于x的函数解析式;
求y关于x的函数解析式;
![]() 当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com