
【题目】如图下图①,等边三角形ABC的边长为2a,CD是AB边上的高,E,F分别是AC和BC边上的点,且满足![]() =k,现将△ABC沿CD翻折成直二面角ADCB,如图下图②.
=k,现将△ABC沿CD翻折成直二面角ADCB,如图下图②.
(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角BACD的正切值.
① ②
②
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)根据AB平行EF即可说明(2)过点D作DG⊥AC于点G,连接BG,可证∠BGD是二面角BACD的平面角,解三角形即可求出.
(1)AB∥平面DEF,
理由如下:在△ABC中,
因为E,F分别是AC,BC上的点,且满足![]() =
=![]() =k,
=k,
所以AB∥EF.
因为AB平面DEF,EF平面DEF,
所以AB∥平面DEF.
(2)如图所示,过点D作DG⊥AC于点G,连接BG.
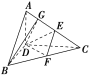
因为AD⊥CD,BD⊥CD,
所以∠ADB是二面角ACDB的平面角.
所以∠ADB=90°,即BD⊥AD.
所以BD⊥平面ADC.
所以BD⊥AC.
所以AC⊥平面BGD.
所以BG⊥AC.
所以∠BGD是二面角BACD的平面角.
在△ADC中,AD=a,DC=![]() a,AC=2a,所以DG=
a,AC=2a,所以DG=![]() =
=![]() =
=![]() .
.
在Rt△BDG中,tan∠BGD=![]() =
=![]() ,即二面角BACD的正切值为
,即二面角BACD的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知命题![]() :
: ![]() 表示双曲线,命题
表示双曲线,命题![]() :
: ![]() 表示椭圆。
表示椭圆。
(1)若命题![]() 与命题
与命题![]() 都为真命题,则
都为真命题,则![]() 是
是![]() 的什么条件?
的什么条件?
(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个)
(2)若![]() 为假命题,且
为假命题,且![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于x 的一元二次方程![]()
(1)若![]() 是从0,1,2,3,4五个数中任取的一个数,
是从0,1,2,3,4五个数中任取的一个数,![]() 是从0,1,2,3四个数中任取的一个数,求上述方程有实数根的概率;
是从0,1,2,3四个数中任取的一个数,求上述方程有实数根的概率;
(2)若![]() 是从区间
是从区间![]() 中任取的一个实数,
中任取的一个实数,![]() 是从区间
是从区间![]() 中任取的一个实数,求上述方程有实数根的概率.
中任取的一个实数,求上述方程有实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() (其中
(其中![]() 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() 为曲线
为曲线![]() 上一点,过点
上一点,过点![]() 作曲线
作曲线![]() 的切线交圆
的切线交圆![]() 于不同的两点
于不同的两点![]() (其中
(其中![]() 在
在![]() 的右侧),已知点
的右侧),已知点![]() .求四边形
.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标![]() 中,设椭圆
中,设椭圆![]()
![]() 的左右两个焦点分别为
的左右两个焦点分别为![]() ,过右焦点
,过右焦点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与椭圆
与椭圆![]() 相交,其中一个交点为
相交,其中一个交点为![]() .
.
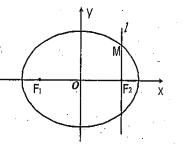
(1)求椭圆![]() 的方程;
的方程;
(2>已知![]() 经过点
经过点![]() 且斜率为
且斜率为![]() 直线
直线![]() 与椭圆
与椭圆![]() 有两个不同的
有两个不同的![]() 和
和![]() 交点,请问是否存在常数
交点,请问是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出
共线?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某综艺节目为增强娱乐性,要求现场嘉宾与其场外好友连线互动.凡是拒绝表演节目的好友均无连线好友的机会;凡是选择表演节目的好友均需连线未参加过此活动的3个好友参与此活动,以此下去.
(Ⅰ)假设每个人选择表演与否是等可能的,且互不影响,则某人选择表演后,其连线的3个好友中不少于2个好友选择表演节目的概率是多少?
(Ⅱ)为调查“选择表演者”与其性别是否有关,采取随机抽样得到如表:
选择表演 | 拒绝表演 | 合计 | |
男 | 50 | 10 | 60 |
女 | 10 | 10 | 20 |
合计 | 60 | 20 | 80 |
①根据表中数据,是否有99%的把握认为“表演节目”与好友的性别有关?
②将此样本的频率视为总体的概率,随机调查3名男性好友,设X为3个人中选择表演的人数,求X的分布列和期望.
附:K2= ![]() ;
;
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,且
,且![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.
的中点.
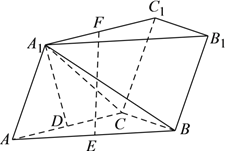
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求证:![]() 平面
平面![]() .
.
(Ⅲ)写出四棱锥![]() 的体积.(只写出结论,不需要说明理由)
的体积.(只写出结论,不需要说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点,
的左、右焦点, ![]() 为双曲线的左顶点,以
为双曲线的左顶点,以![]() ,
, ![]() 为直径的圆交双曲线某条渐近线于
为直径的圆交双曲线某条渐近线于![]() ,
, ![]() 两点,且满足
两点,且满足![]() ,则该双曲线的离心率为________.
,则该双曲线的离心率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合P={(x,y)||x|+|y|≤1,x∈R,y∈R},Q={(x,y)|x2+y2≤1,x∈R,y∈R},R={(x,y)|x4+y2≤1,x∈R,y∈R}则下列判断正确的是( )
A.PQR
B.PRQ
C.QPR
D.RPQ
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com