
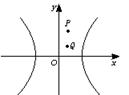
已知双曲线C:2x2-y2=2与点P(1,2)
(1)求过P(1,2)点的直线l的斜率取值范围,使l与C分别有一个交点,两个交点,没有交点.
(2)若Q(1,1),试判断以Q为中点的弦是否存在.
(1)当k=±![]() ,或k=
,或k=![]() ,或k不存在时,l与C只有一个交点;当
,或k不存在时,l与C只有一个交点;当![]() <k<
<k<![]() ,或-
,或-![]() <k<
<k<![]() ,或k<-
,或k<-![]() 时,l与C有两个交点;当k>
时,l与C有两个交点;当k>![]() 时,l与C没有交点.
时,l与C没有交点.
(2)Q为中点的弦不存在.
(1)当直线l的斜率不存在时,l的方程为x=1,与曲线C有一个交点.当l的斜率存在时,设直线l的方程为y-2=k(x-1),代入C的方程,并整理得
(2-k2)x2+2(k2-2k)x-k2+4k-6=0
(ⅰ)当2-k2=0,即k=±![]() 时,方程有一个根,l与C有一个交点
时,方程有一个根,l与C有一个交点
(ⅱ)当2-k2≠0,即k≠±![]() 时
时
Δ=[2(k2-2k)]2-4(2-k2)(-k2+4k-6)=16(3-2k)
①当Δ=0,即3-2k=0,k=![]() 时,方程有一个实根,l与C有一个交点.
时,方程有一个实根,l与C有一个交点.
②当Δ>0,即k<![]() ,又k≠±
,又k≠±![]() ,故当k<-
,故当k<-![]() 或-
或-![]() <k<
<k<![]() 或
或![]() <k<
<k<![]() 时,方程有两不等实根,l与C有两个交点.
时,方程有两不等实根,l与C有两个交点.
③当Δ<0,即k>![]() 时,方程无解,l与C无交点.
时,方程无解,l与C无交点.
综上知:当k=±![]() ,或k=
,或k=![]() ,或k不存在时,l与C只有一个交点;
,或k不存在时,l与C只有一个交点;
当![]() <k<
<k<![]() ,或-
,或-![]() <k<
<k<![]() ,或k<-
,或k<-![]() 时,l与C有两个交点;
时,l与C有两个交点;
当k>![]() 时,l与C没有交点.
时,l与C没有交点.
(2)假设以Q为中点的弦存在,设为AB,且A(x1,y1),B(x2,y2),则2x12-y12=2,2x22-y22=2两式相减得:2(x1-x2)(x1+x2)=(y1-y2)(y1+y2)
又∵x1+x2=2,y1+y2=2
∴2(x1-x2)=y1-y1
即kAB=![]() =2
=2
但渐近线斜率为±![]() ,结合图形知直线AB与C无交点,所以假设不正确,即以Q为中点的弦不存在.
,结合图形知直线AB与C无交点,所以假设不正确,即以Q为中点的弦不存在.


科目:高中数学 来源: 题型:
 已知双曲线C:2x2-y2=2与点P(1,2)
已知双曲线C:2x2-y2=2与点P(1,2)查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013届云南大理宾川县四中高二1月月考文科数学试卷(解析版) 题型:解答题
已知双曲线C:2x2-y2=2与点P(1,2).求过点P(1,2)的直线l的斜率k的取值范围,使l与C只有一个交点;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
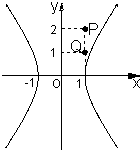 已知双曲线C:2x2-y2=2与点P(1,2)
已知双曲线C:2x2-y2=2与点P(1,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com