
设函数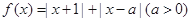
(1)若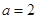 时,解不等式
时,解不等式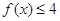 ;
;
(2)若不等式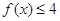 的对一切
的对一切 恒成立,求实数
恒成立,求实数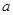 的取值范围
的取值范围
(1) (2)
(2)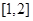
解析试题分析:(1)可以采用零点分段法或者绝对值的定义来解决该绝对值不等式,其中零点分段法即把x分为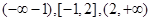 三段讨论去掉绝对值来求的该不等式的解集,而绝对值的定义,即
三段讨论去掉绝对值来求的该不等式的解集,而绝对值的定义,即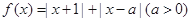 表示在数轴上点x到-1和a的距离之和,利用数轴即可得到相应的解集
表示在数轴上点x到-1和a的距离之和,利用数轴即可得到相应的解集
(2)首先由区间的a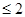 ,再根据x的范围去掉绝对值,剩下即为恒成立问题,再利用分离参数法分离x与a,求出x一边的最值即可.解得a的范围.
,再根据x的范围去掉绝对值,剩下即为恒成立问题,再利用分离参数法分离x与a,求出x一边的最值即可.解得a的范围.
试题解析:
(1)由题得a=2,
法一.利用绝对值的定义,即|x+1|即为在数轴上x与-1之间的距离,|x-2|是x与2之间的距离.故利用数轴法可以求的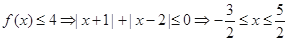 ,综上
,综上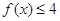 的解集为
的解集为 .
.
法二.零点分段法,分为一下三种情况
当x>2时, 
当-1 x
x 2时,
2时, 
当x<-1时, 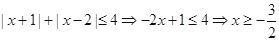
综上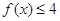 的解集为
的解集为 .
.
(2)由题得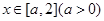 ,所以
,所以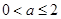 且
且 ,即
,即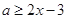 在区间
在区间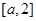 上恒成立,所以
上恒成立,所以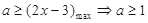 ,综上a的取值范围为
,综上a的取值范围为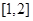 .
.
考点:绝对值不等式 恒成立问题


 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
某公司欲建连成片的网球场数座,用288万元购买土地20000平方米,每座球场的建筑面积为1000平方米,球场每平方米的平均建筑费用与所建的球场数有关,当该球场建n座时,每平方米的平均建筑费用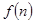 表示,且
表示,且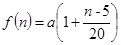 (其中
(其中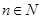 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.
(1)为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几座网球场?
(2)若球场每平方米的综合费用不超过820元,最多建几座网球场?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com