练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设
    e1
    ，
    e2
    是平面内两个不共线的向量，
    AB
    =（a-1）
    e1
    +
    e2
    ，
    AC
    =b
    e1
    -2
    e2
    （a＞0，b＞0），若A，B，C三点共线，则
    1
    a
    +
    2
    b
    的最小值是（　　）
    A、2B、4C、6D、8
    分析：利用向量共线定理推出a，b的关系，进而解出
    1
    a
    +
    2
    b
    的最小值
    解答：解：∵A，B，C三点共线，
    ∴
    AB
    ，
    AC
    共线，
    ∴存在实数λ，使得
    AB
    =λ
    AC

    可解得λ=-
    1
    2
    ，b=2-2a
    ∵a＞0，b＞0∴0＜a＜1
    ∴
    1
    a
    +
    2
    b
    =
    1
    a
    +
    1
    1-a
    =
    1
    a(1-a)

    当a=
    1
    2
    时，取最小值为4
    故选：B．
    点评：本题主要考察了向量的共线定理，属于中等题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设
    e1
    ，
    e2
    是平面内一组基向量，且
    a
    =
    e1
    +2
    e2
    ，
    b
    =-
    e1
    +
    e2
    ，则
    e1
    +
    e2
    =λ1
    a
    +λ2
    b
    ，则λ1+λ2=
    1
    3
    1
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•普陀区二模）设
    e1
    、
    e2
    是平面内一组基向量，且
    a
    =
    e1
    +2
    e2
    、
    b
    =-
    e1
    + 
    e2
    ，则向量
    e1
    +
    e2
    可以表示为另一组基向量
    a
    、
    b
    的线性组合，即
    e1
    +
    e2
    =
    2
    3
    2
    3
    a
    +
    -
    1
    3
    -
    1
    3
    b
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设
    e1
    、
    e2
    是平面内两个不平行的向量，若
    a
    =
    e1
    +
    e2
    与
    b
    =m
    e1
    -
    e2
    平行，则实数m=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

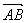
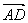
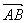
    设e1、e2是平面内的一组基底,如果=3e1-2e2,=4e1+e2, =8e1-9e2,求证:A、B、D三点共线.

    查看答案和解析>>

    同步练习册答案